前言:PEFT的诞生
传统的预训练-下游任务微调的范式,是对预训练模型所有参数进行微调,即全量微调。之前基于Bert、GPT1的下游微调任务都是这么干的。因为当时的预训练模型参数量比较少,所以速度并没有那么慢。但是自从GPT2诞生之后,后边出现的模型越来越大,参数量越来越多。这个时候进行全量微调就有很明显的劣势了,训练时间长不说,显存还容易爆。在这个背景下,PEFT(Parameter-Efficient Fine-Tuning)就诞生了。
实际上,在Lora诞生之前,已经诞生过一些PEFT方法了,只是Lora以及它的各种变体是比较好用的那个。Lora原论文中的baseline部分提到了之前有的一些PEFT方法:

我们大概看一眼:
Bias-only or BitFit: 只更新bias,其他参数都冻住 Prefix-embedding tuning (PreEmbed):这个方法又称为Prompt Tuning在输入tokens中插入一些特殊的tokens,这些tokens是词表外的tokens.训练的时候只训练这些特殊tokens的嵌入向量。而这个插入的方式又分为prefix和infix,分别表示插入到原始tokens的前面或者中间。所以需要更新的参数量为 。指的是prefix和infix的数量。 Prefix-layer tuning (PreLayer):是上边这种方法的扩展。上边只在最开始的word embeddings中插入。这种方式就是在每个transformer层中间都会插入,所以对应的参数量就变为了: Adapter tuning:一张图就可以解释明白
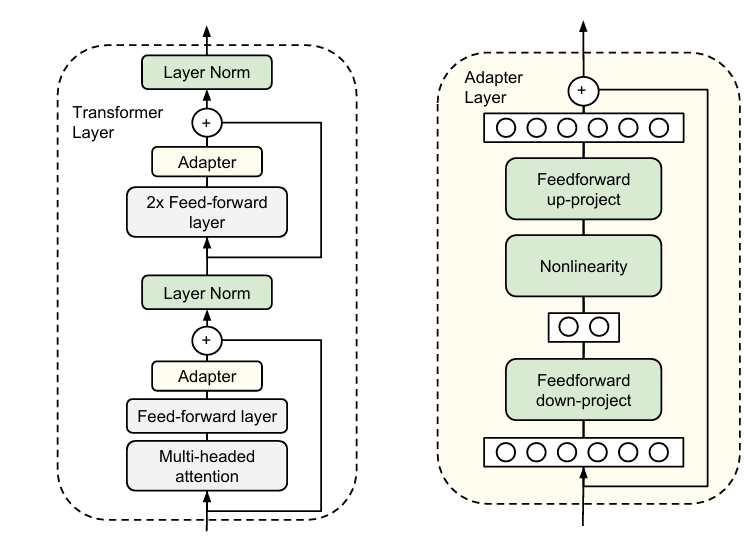
在每个transformer层中的多头注意力层和FNN层之后加一个adapter层,所谓adapter层就是一个降维再升维度。在对大模型训练的时候,其他层都冻住,只训练这个adapter层。我理解的adapter层的作用就是总结前边模块的东西。
通过这些已有的PEFT方法,我们发现一个他们的共同点:就是将大模型的所有参数都先冻住,之后注入一些东西,这个东西是带有参数的,训练的时候只训练我们注入的参数。就能达到比较好的效果。Lora也是类似的思路,先将所有参数都冻住,然后注入一些可以更新的东西。但是这个注入的东西是什么,就大有讲究了
Lora的工作过程
Lora原论文写到:
Many sought to mitigate this by adapting only some parameters or learning external modules for new tasks. This way, we only need to store and load a small number of task-specific parameters in addition to the pre-trained model for each task, greatly boosting the operational efficiency when deployed. However, existing techniquesoften introduce inference latency (Houlsby et al., 2019; Rebuffi et al., 2017) by extending model depth or reduce the model’s usable sequence length (Li & Liang, 2021; Lester et al., 2021; Hambardzumyan et al., 2020; Liu et al., 2021) (Section 3). More importantly, these method often fail to match the fine-tuning baselines, posing a trade-off between efficiency and model quality.
Lora的作者提到:method often fail to match the fine-tuning baselines,posing a trade-off between efficiency and model quality.
之前的PEFT方法只能在效率与模型质量之间权衡。
我们通过观察发现之前的微调方法基本都是对原本模型中的一些地方懂一些手脚,无论是注入一个额外的MLP层,或者是注入一个词向量矩阵层。但这些方法,无一例外,注入的层都没法完完全全match原始模型的所有参数,他们注入的东西更多的是对大模型层的一个summary。那肯定会丢东西的。
所以Lora要做的就是:效率与模型质量我全都要!。
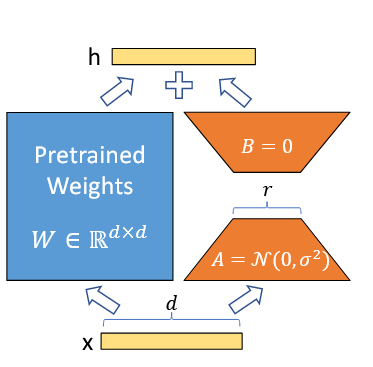

Lora的全称是:LOW-RANK-PARAMETRIZED UPDATE 低秩参数更新。
大模型的参数都是来源于各个模块的参数矩阵,例如 attention 的 MLP 的 、还有embedding层的。
而每个更新时:
Lora的思路就是:
将分解为两个低秩矩阵。其中
之后就只需要更新两个参数即可。 这里的就是A、B矩阵的秩
因此额外的可训练参数量由原来的,减小到:
,文中提到 所以能极大减少训练参数量。
举个例子,如果的大小为,即。如果全量微调,就需要更新个参数。但是经过低秩分解,假设,则分解为:.需要更新的参数是:。足足少了256倍。
在实际训练中,我们会将矩阵冻住,然后注入矩阵,在反向传播更新参数的时候,只更新矩阵,最后保存B、A矩阵,之后推理的时候就直接计算:
这么做的好处就是它可以按需加载多个 LoRA Adapter,并且不需要改变原模型结构。一个基础模型可以对不同的下游任务训练不同的 LoRA Adapter,而 LoRA Adapter又很小。很容易保存。
Lora的数学原理
一个矩阵那么多参数量,这直接少了这么多参数,难道不会丢失很多信息吗?首先,丢肯定是会丢的,无论是lora,还是前面提到的那些PEFT方法,都会丢信息,但是Lora为什么比前面的有效?。这其中是有数学原理支撑的。原文中写到:
A neural network contains many dense layers which perform matrix multiplication. The weight matrices in these layers typically have full-rank. When adapting to a specific task, Aghajanyan et al. (2020) shows that the pre-trained language models have a low “instrisic dimension” and can still learn efficiently despite a random projection to a smaller subspace.
对于一个参数矩阵,他一般是满秩的,满秩就代表着这里面所有信息都是有用的。但是后边又说了,当处理下游任务时,它可以以一个低秩来处理信息,就是满秩矩阵他用不到所有的秩,只需要一些子空间就可以高效的处理子任务。
这个数学原理是什么?这就要提到奇异值分解(SVD)
这里大概说一下什么是奇异值分解。在线性代数中,我们知道对于一个矩阵M可以求出他的特征值和特征向量:
求出了所有特征值和特征向量,如果这些特征向量都线性无关,我们就可以将他的所有特征向量拼成一个矩阵,然后所有特征值放到对角线拼成一个矩阵。可以将矩阵分解为:
之后也可以进一步将特征矩阵向量标准化,进而得到:
总之就是可以将他分解成三个矩阵。但是这样的分解方式仅限于方阵,对于非方阵,我们也有一个方法可以对他进行分解,就是奇异值分解(SVD)
对任何一个矩阵,我们可以对他做奇异值分解:
其中:
关于SVD的详细分解过程,可以参考以下博客:
https://www.cnblogs.com/pinard/p/6251584.html
奇异值分解出的矩阵有一个很重要的性质:对角线的奇异值是逐渐减小,并且减小的特别快。很多情况下,前几个奇异值就占了很大的一部分,后边的奇异值小到可以忽略不计。
举个例子
对于矩阵S:
我们对它进行奇异值分解得到:(以下结果来自ChatGPT 5.1 thinking)

可以看到这5个奇异值,第四个和第五个就很小了,如果我们只取前3维,对应的和也取相应的前三行和前三列
计算
得到:
可以看到和原矩阵非常接近。
也就是说,奇异值分解得到的矩阵,可以取他们各自的低秩矩阵,来逼近原始的矩阵。
因为对角线的奇异值是逐渐减小,并且减小的特别快。很多情况下,前几个奇异值就占了很大的一部分,后边的奇异值小到可以忽略不计。所以当原始矩阵非常大的时候,我们就可以做到以非常低秩的矩阵来逼近原始的矩阵,并且保证误差不会很大。
所以这就引出了lora的数学原理:
对于任意一个矩阵我们都可以进行奇异值分解(SVD):
其中:
和 是正交矩阵。的对角线上是奇异值,按从大到小排列。又因为的性质,所以我们可以只取前个最大的奇异值,得到:
这里的维度为,维度为 ,为。
由于是对角矩阵,我们可以对其开平方:
于是我们定义:
就有:
我用我的大白话总结一下就是:
由SVD可知,任何一个m×m矩阵,都可以做SVD分解,分解成 三个矩阵,如果将三个矩阵取前r行,即进行相乘,最后得到的矩阵也能逼近原始矩阵,之后将这三个矩阵转成两个,即将中间的矩阵开平方(因为这个矩阵是只存在对角线的奇异值,所以将对角线上的元素开平方即可得到两个矩阵相乘),然后分别乘给矩阵,矩阵,最后得到两个矩阵,若最开始的矩阵为为m×m 则就可以看作近似逼近然后更新参数的时候只需要分别更新,即可