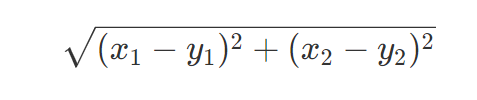什么是决策树
在生活中,我们经常利用决策树这种算法,比如,判断今天要不要去上课,如果犯懒了,那就不去,如果不懒,则再判断这节课要不要点名,如果不点名,那就不去,如果点名,那再判断这节课是不是水课,如果是水课,那就不去,如果不是水课,那就去。以上也可以用if else来表示:
if 犯懒:
不去
else:
if 不点名:
不去
else:
if 是水课:
不去
else:
去这正好是一种树结构:
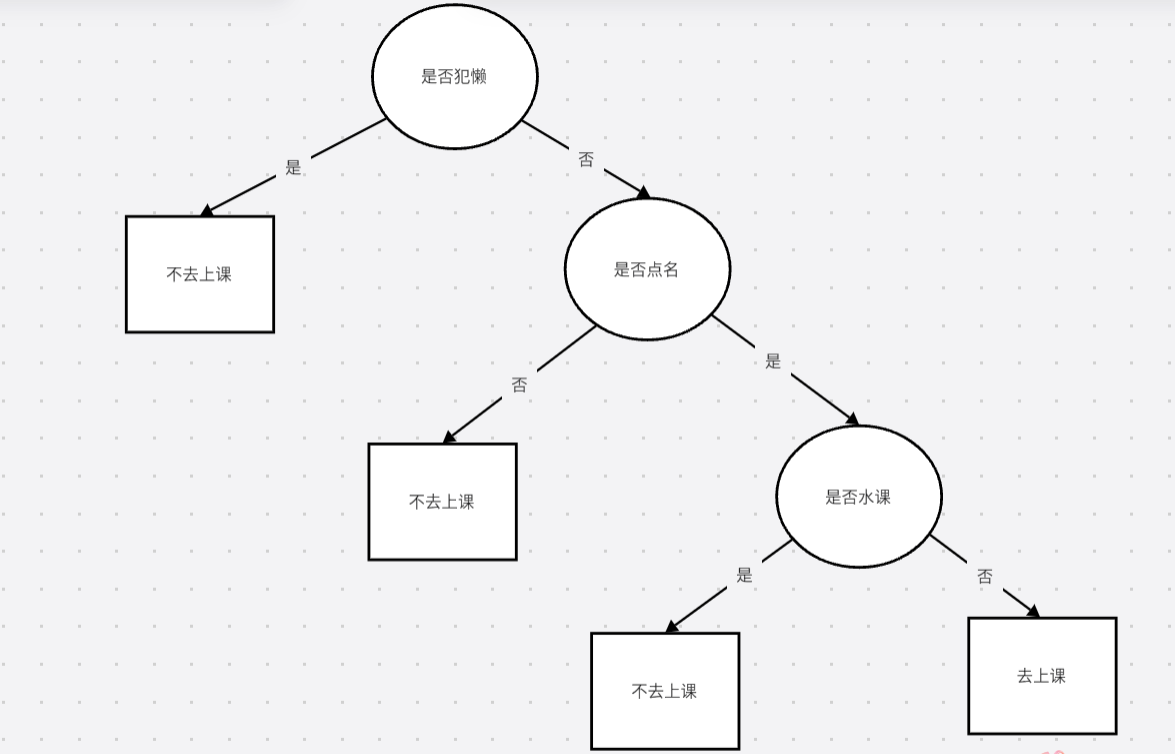
在这个例子中,我先考虑了自己是否犯懒,然后考虑是否点名,最后考虑了是不是水课,这些就是我所考虑的条件,对应到模型中就是输入空间的特征值。刚才的例子中如果我先考虑是否点名,再考虑其他两个,得出的树模型就会不同,他们的泛化能力也会有所不同。
这么多特征值,我们先考虑哪个呢?有的特征需要考虑吗?要考虑的特征中,他们要考虑的先后顺序是什么?
以上的问题,就是构建决策树模型中,我们要解决的问题,这个问题叫做划分选择
划分选择
着决策树深度的不断增加,我们希望分支两头的节点所包含的样本尽量所属于一个类别,就是希望每次的划分力度更高。再换句话说,我们希望每次分类都能分成两批不属于同一类别的样本,即划分的节点的纯度更高。
信息增益
首先要了解什么是信息熵
信息熵
信息熵是信息理论中用于衡量随机变量不确定度的概念,就是表示随机变量内部的混乱程度的。熵越大,内部越混乱
假设随机样本X中第i类样本所占比例为$p(x_i)$
则X的信息熵定义为
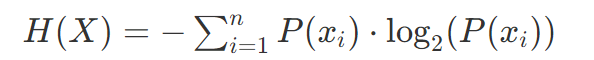

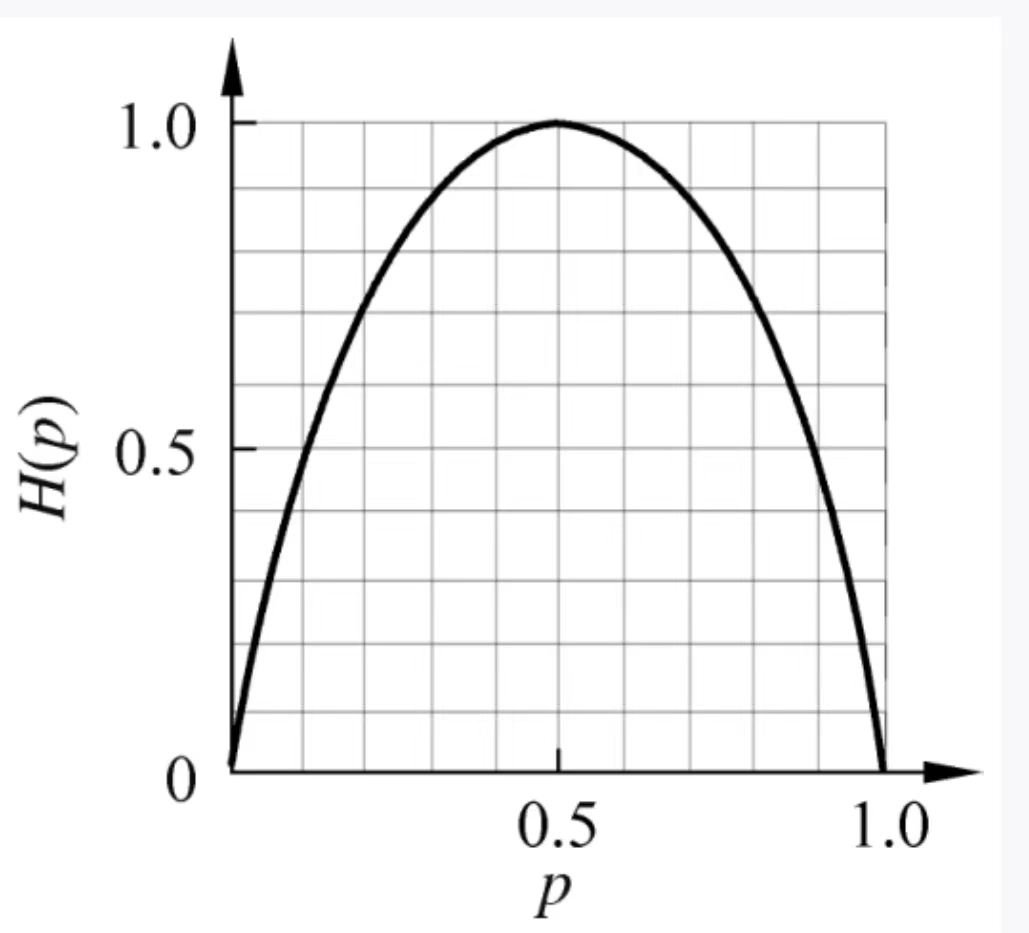
可以看到,当p取0.5的时候,熵值最大。(其实对于多个值,当各个变量X的概率p的取值相等时候,H(p)就是最大的)。
这里直接讲什么是信息增益有些抽象,先来以一组数据来讲解
信息增益的例题
以下图该数据为例
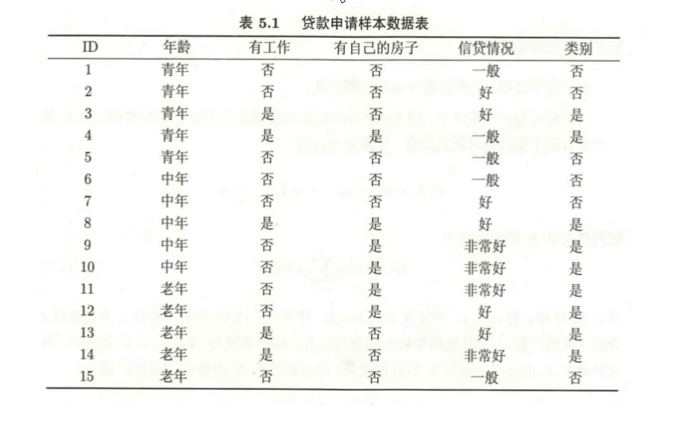
在我们构建决策树的过程中,首先要确定根节点,确定根节点之前,我们先计算输出值Y的信息熵

由图可得
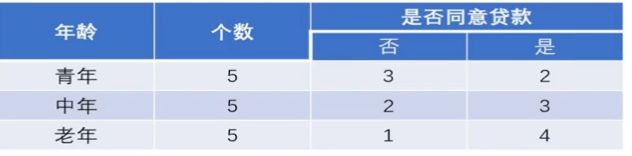

这层并不是根节点,是决策树的第一层,所以我们需要计算加权信息熵,也就是:
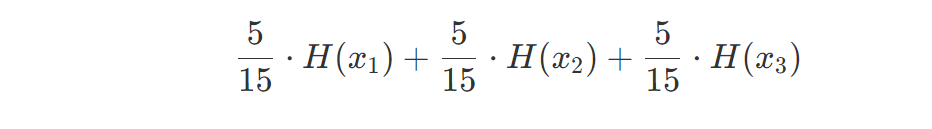
这里算出结果为0.888。
同理我们接着算其他特征的加权信息熵。
得出是否有自己的工作这个特征的加权信息熵为0.647。是否有自己的房子这个特征的加权信息熵为0.551。信贷情况为0.608。
这时候我们用前面算出的信息熵分别减去这三个加权信息熵可以得到各自的信息增益了:
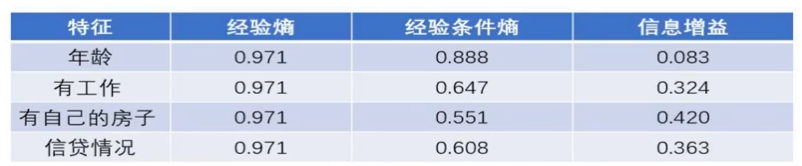
我们前面根据Y算出的那个信息熵,学名叫做经验熵,记作$H(X)$后边这个加权信息熵,经验条件熵,记作$H(Y|X)$它度量了我们的X在知道Y以后剩下的不确定性,而信息增益,就是用经验熵-经验条件熵:
$H(X)-H(Y|X)$
需要注意的是,我们这里用$H(X)$表示,X表示特征而不是测试集,在我们计算的时候,是带入的Y,这里的Y和X本质上都是特征,只是一个是输入特征,一个是输出特征。在决策树的第一层建立的时候,我们的经验熵是用Y特征来计算,在第一层建立好之后,计算第二层的时候,就不用Y了,而是继续用X中的特征。
基于信息增益的ID3算法
ID3算法是一种贪心算法,用于构造决策树。ID3算法起源于概念学习系统(CLS),以信息熵的下降速度为选取测试属性的标准,即在每个节点选取还尚未被用来划分的具有最高信息增益的属性作为划分标准,然后继续这个过程,直到生成的决策树能完美分类训练样例。
ID3算法的核心思想是:在所有属性中,选择能够将数据集划分成具有最小熵的属性作为划分标准。 这句话的意思就是选择当前特征下最大信息增益的特征。
算法过程:

光看过程还是很抽象,我们看个例子吧

还是刚才的数据集
我们刚才已经计算了第一层了

可以看到"有自己的房子"这一特征的信息增益最大,然后判断该信息增益是否比我们的阈值ε大,这里这个ε就是一个超参,需要我们自己设置,假设我们设置ε为0.010.那我们就选择该特征为决策树的第一层。
选择了第一层后,会形成两个分支,那就是拥有自己的房子和没有自己的房子。
在拥有自己的房子这个分支中:

可以看到输出特征全部都是同意贷款,这就符合了我们算法中:"若D中所有实例属于同一类,则T为单结点树,记录实例类别Ck,以此作为该结点的类标记,并返回T"这一步
所以拥有自己的房子这个分支就直接返回同意贷款,接着另一边的分支并不是都同意贷款,那么我们这个分支。就要继续进行计算信息增益,继续划分。到这一步,我们生成的决策树为:

接下来,我们继续计算右边节点的信息增益
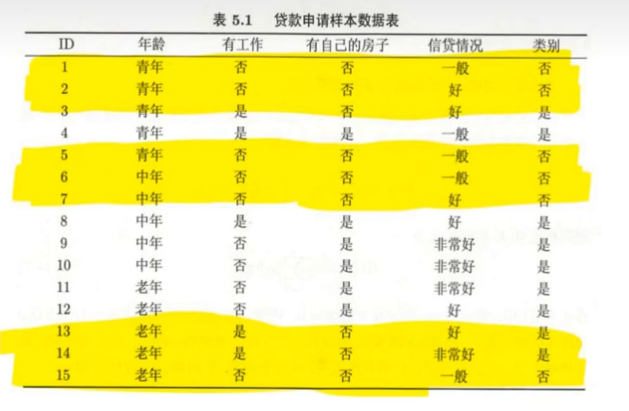
因为上一步已经筛掉了拥有自己房子的人,所以接下里我们只需要计算未拥有自己房子的人。只剩下了9个样本。
首先我们计算经验熵:
上一层我们计算经验熵是以输出特征"是否同意贷款"来确定的,因为那里是根节点,但是到了这一层,因为我们的第一层是"是否有自己的房子",所以我们需要该特征来计算经验熵:

可以看到没有自己的房子的人里,有6个同意贷款的,3个不同意的:这里将"是否有自己的房子"这个特征记作$X_1$
所以经验熵为:
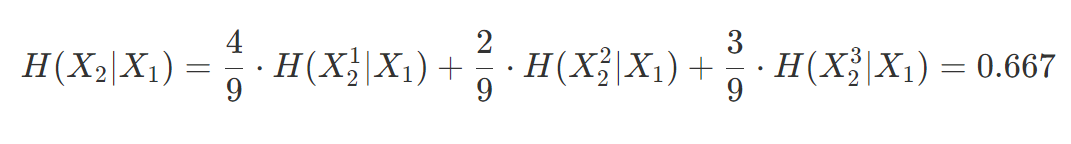
然后我们先计算"年龄"特征的经验条件熵。
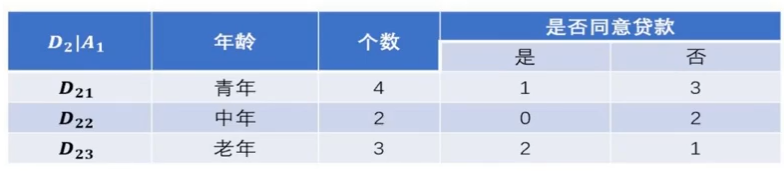
将年龄这个特征记作$X_2$
将老年、中年、青年分别记为$X_2^1、X_2^2、X_2^3$
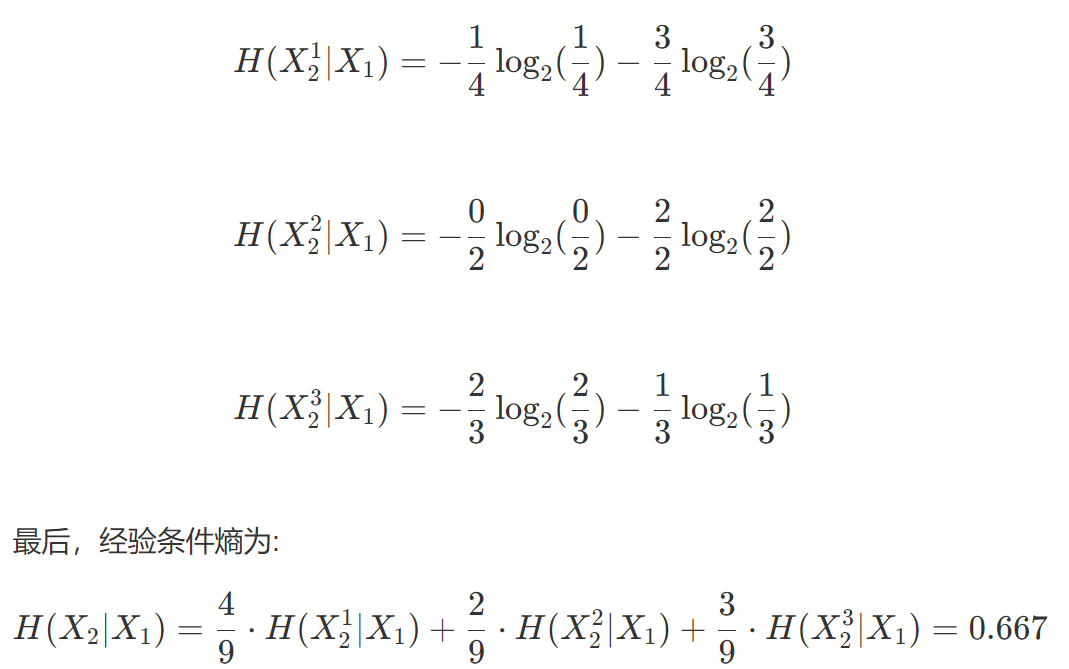
同理,我们可以算出其他几个特征:
是否有工作的经验条件熵为:0,信贷情况:0.444
然后计算每个特征的信息增益:

我们得出是否有工作这个信息增益最大,所以我们选择是否有工作这个特征作为下一层。
同理,我们判断一下有工作这个特征所对应的输出特征Y是否为同一类

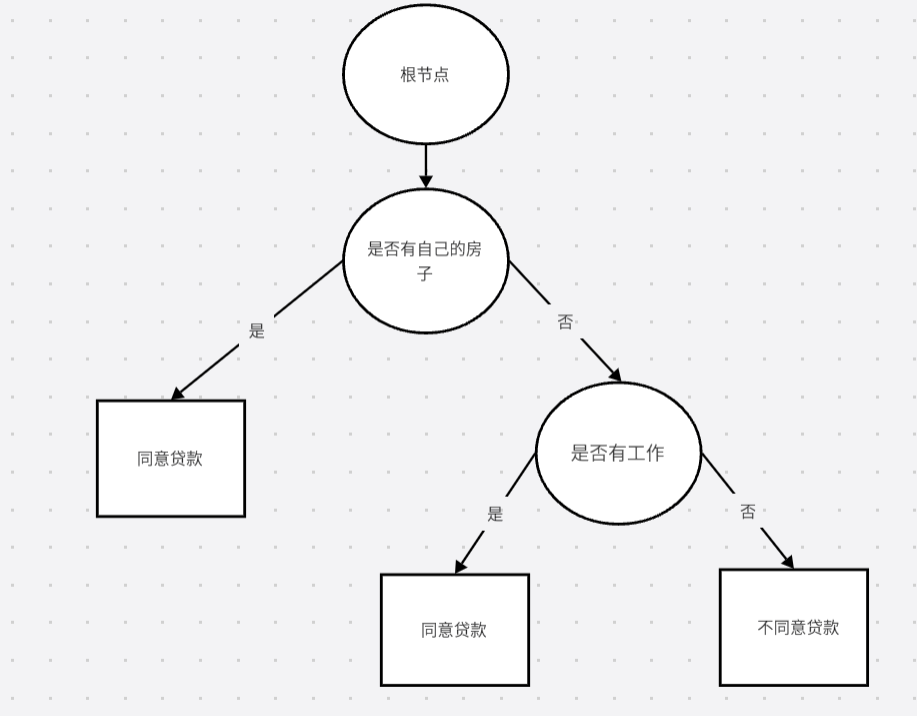
可以看到两个分支所得到的Y都是是都属于同一类的,所以我们这颗决策树到这里就为止了。就构建完成了,得到的决策树为:
信息增益比(增益率)
但是基于信息增益的ID3算法也是有缺点的。在相同条件下,拥有更多取值的特征的信息增益更大,信息增益的计算会受到属性取值数量的影响。具有更多取值的属性往往有更高的信息增益,因为它们有更多的可能性来区分数据。这可能导致算法偏向于选择具有大量取值的属性。
这时候就有人提出了信息增益比的概念

因为信息增益的缺点为拥有更多取值的特征的信息增益更大,在信息增益比中,当特征值增加时,分母对应的该特征值的熵越大,可以平衡掉分子的增大。
基于信息增益比的C4.5算法
关于C4.5算法的算法过程和ID3并没有多大区别,只是将信息增益换成了信息增益比:

ID3算法和C4.5算法的不足
- ID3算法和C4.5算法对于处理连续值都不太友好,就算将连续值离散化,可能会引入信息损失,并且不够灵活。
- 计算复杂度高,因为都需要进行熵值计算,里面有大量的耗时的对数运算。
- 生成的是多叉树,即一个父节点可以有多个节点。很多时候,在计算机中二叉树模型会比多叉树运算效率高。如果采用二叉树,可以提高效率。
小结
决策树真是一个细节满满的模型,一篇文章记录不下。。。
下一篇文章总结一下效率更高的CART算法以及决策树的剪枝