RNN所解决的问题
RNN是专门处理具有序列关系的输入数据而诞生的网络,它能挖掘数据中的时序信息以及语义信息
序列关系数据
什么是具有序列关系的数据呢? 主要就是符合时间顺序,逻辑顺序等顺序的数据。例如 天气预报,一般天气预报都是通过前几天的数据特征,例如温度、气压等来预测今天的天气,这是一种时间序列关系的数据,而人类的自然语言,是符合某种逻辑规则的词组成的,我们在读一句话的时候,理解当前词的时候都是根据前边的词,没有人思考的时候是将前面的词都丢掉,所以自然语言也是一种序列数据。
但是传统的神经网络是很难根据一个序列前面的信息来得到当前序列的值。这个时候RNN就诞生了。
RNN的结构
RNN的大体流程
RNN中有一个非常重要的结构:RNN Cell
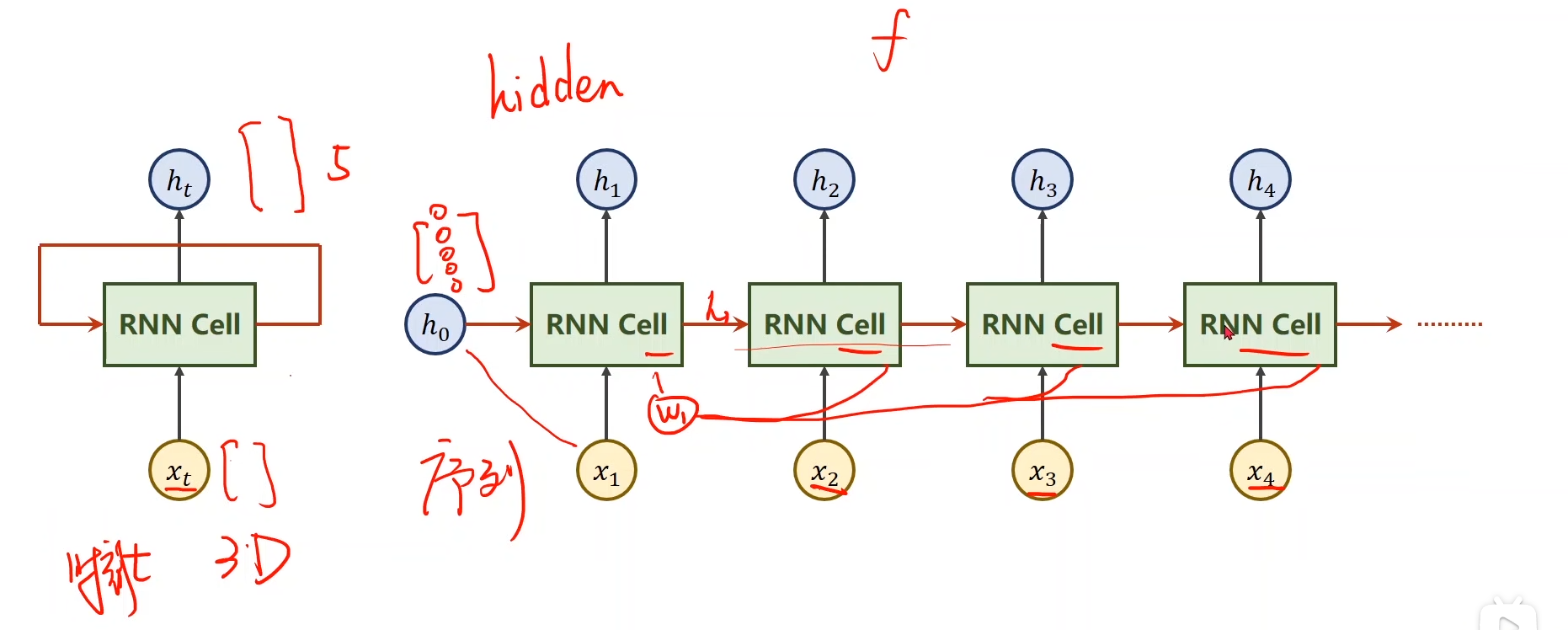
刘二大人这个教程的图片非常清晰,RNN cell的作用是将输入x线性转换成一组新的向量,但是这个RNN cell和一般的线性层还不一样,我们这个线性层会将每一个x考虑进来,它是按时间顺序将每一个 和先前状态 一起输入 RNN cell,递归地计算当前状态 ,从而逐步“记忆”序列信息。,之后将生成的和一并输入到RNN cell中来生成。
图中的是先验知识,例如,当我们的任务是通过图像生成文本,那么就可以利用CNN+全连接生成,如果没有先验,那就将设为全0.
如果用代码理解一下就是:
h=0
X=[1,3,2,5,4]
for x in X:
h=linear(x,h)
所以该网络叫做循环神经网络
那生成之后要干什么呢?
到实际上就是对每一个输入向量进行再次处理,使每一个都能考虑到前面输入的,生成一个含有序列信息的向量
即生成的到的就是对应的最终转换成的向量,即对于:
那么每一个就将当前输入的通过序列的方式全部考虑了进来。如下图所示
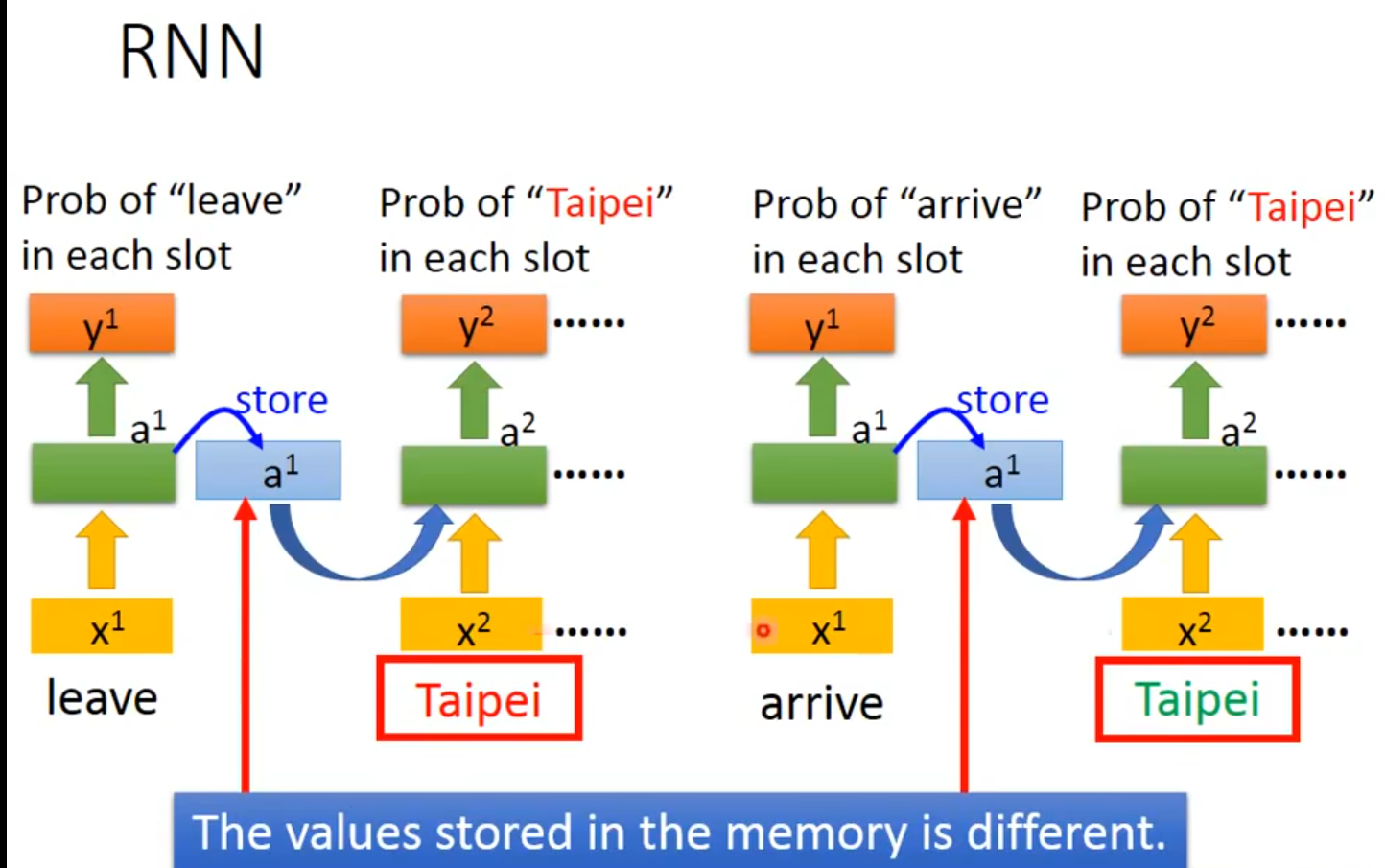
RNN CELL的具体计算过程
那RNN cell中到底是什么呢?
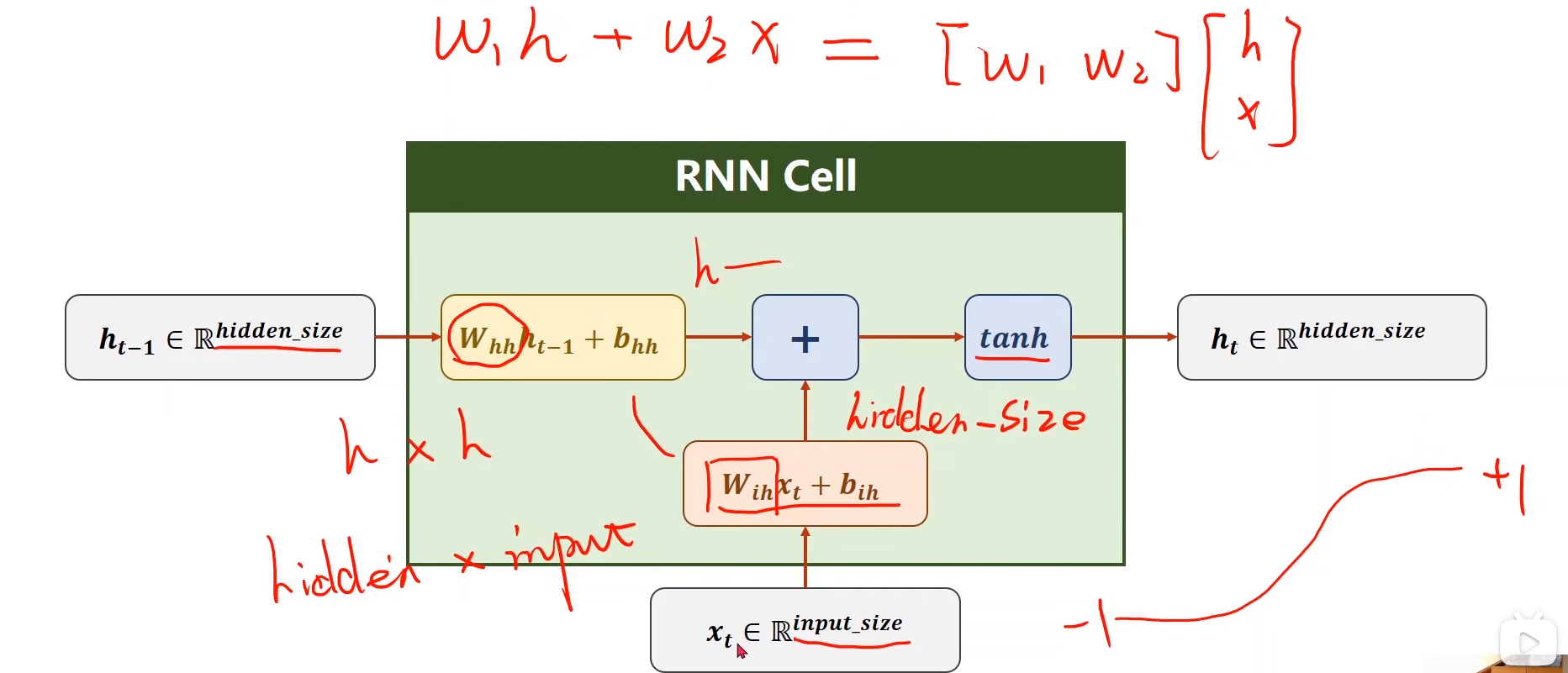
其实就是一个简单的线性相加,将每一个和相加,在实际上运算时,们可以将 和 拼接为一个向量,然后拼接相应的权重矩阵,统一成一次线性变换,即:
其中 的维度是 h的维度×(x维度+h维度),在torch.nn.RNN中即为(hidden_size, input_size + hidden_size),这种方式在执行起来更高效。
关于权重矩阵的下标与含义:
指的权重矩阵.下标是的原因是该矩阵是到的线性变换的权重。
则指的是的权重矩阵。该矩阵是到的线性变换的权重。之后将这两个加起来就可以得到最终的
所以的维度就是h×h,在torch.nn.RNN中即为:(hidden_size, hidden_size),而的维度为(hidden_size, input_size)
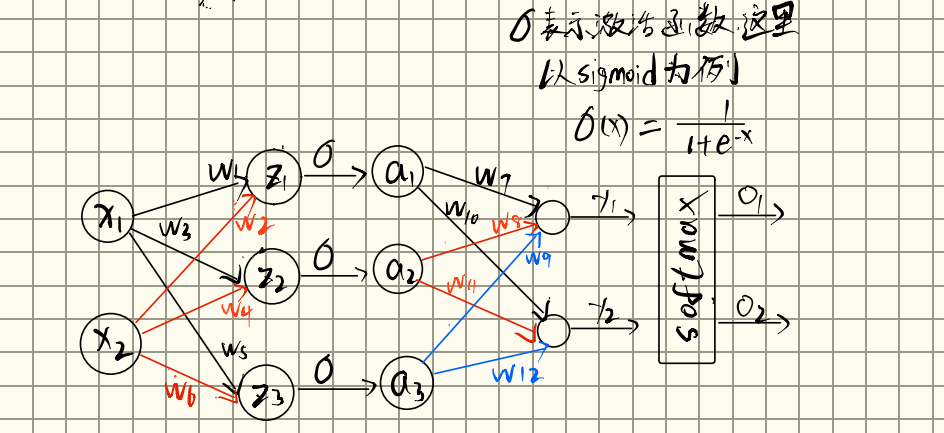
所以RNN Cell的公式为:
为激活函数,在RNN中,常用,它可以将输出值压缩到(-1,1)之间
所以整个RNN最终就是一个这么个过程:
现在以一个例子来说明(例子中都省去了偏执)
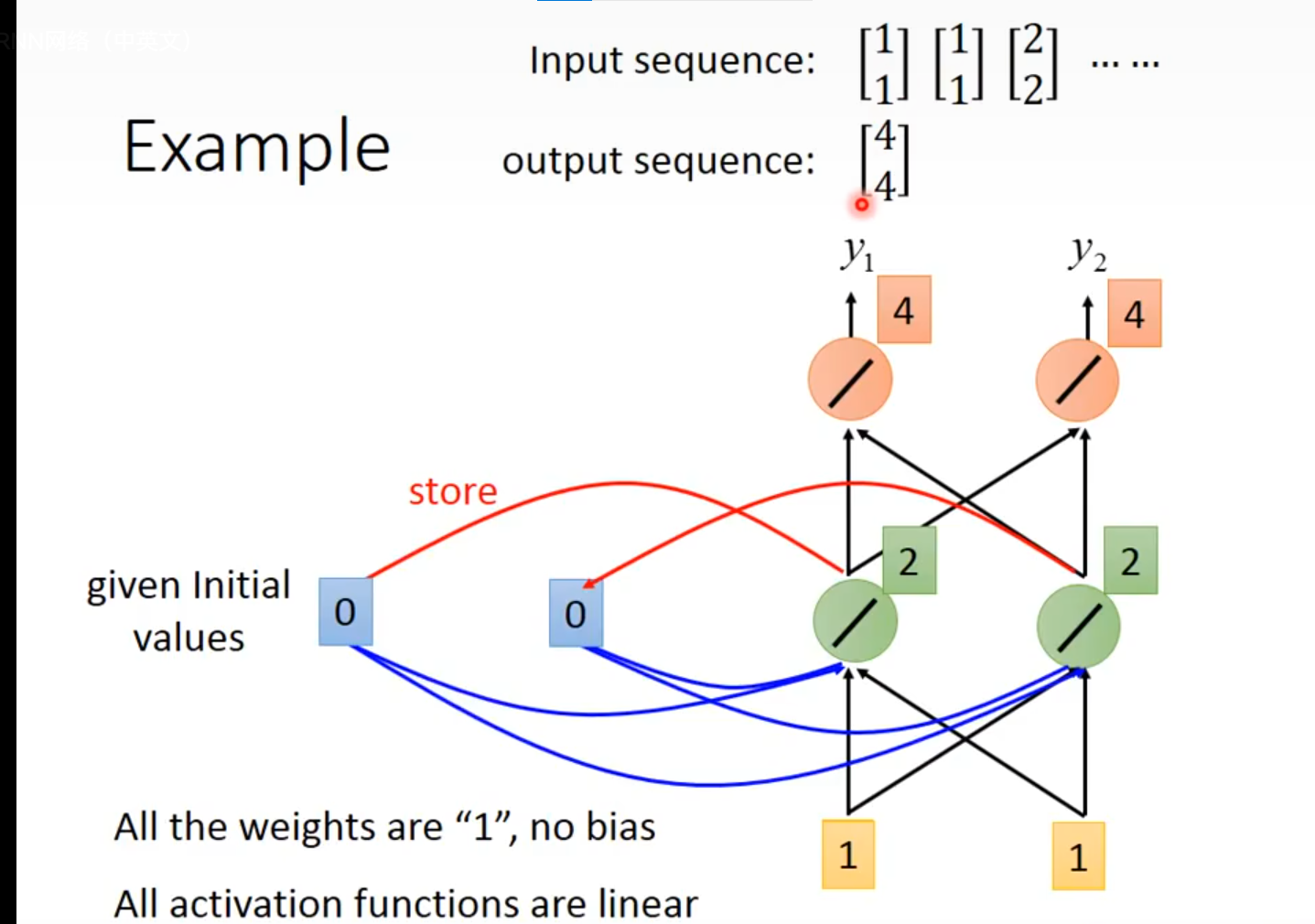
现输入一个句子,将句子转换为向量之后:
input sequence :
我们对每一个输入的向量进行处理
输入向量的维度为2,则我们令初始化为,并假设将所有的权重初始化为"1"(实际工作中不会这么干,这里为了方便计算)
这里的都初始化为"1",所以得到:
现补的知识点:对于y=wx 若输入的每个x向量维度为n,且线性变换之后的y向量维度为m, 则权重w矩阵的维度为m×n,因为这里我们让初始化为,维度为2,所以的维度就等于h的维度乘以h的维度,为2×2,而的维度等于输入x的维度乘以h的维度,这里我们的输入向量的维度恰好也为2,所以权重矩阵的维度就是2×2
首先我们处理第一个输入向量:
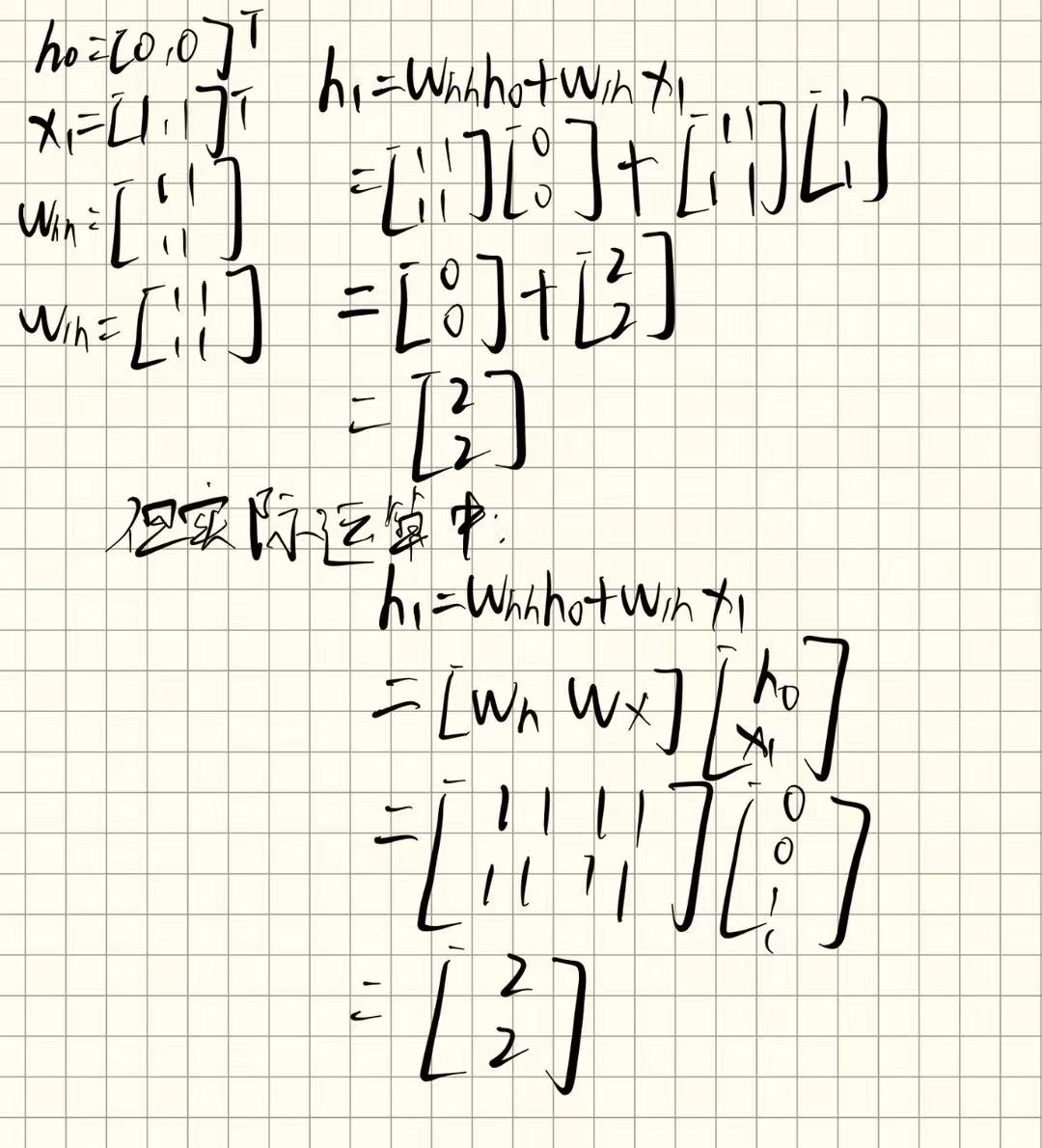
得到,接下来:
其中,依然为"1"。
和上边的计算过程一样,得到
同理
其中
所以
以此类推,我们可以得到
RNN CELL的DEEP用法
上边的例子中,RNN CELL只是简单的一个线性相加,只有一层,
为什么要用表示输入线性转换成的新向量?实际上表示hidden的意思,既然是隐藏层了,我们当然可以将这个层数加深。
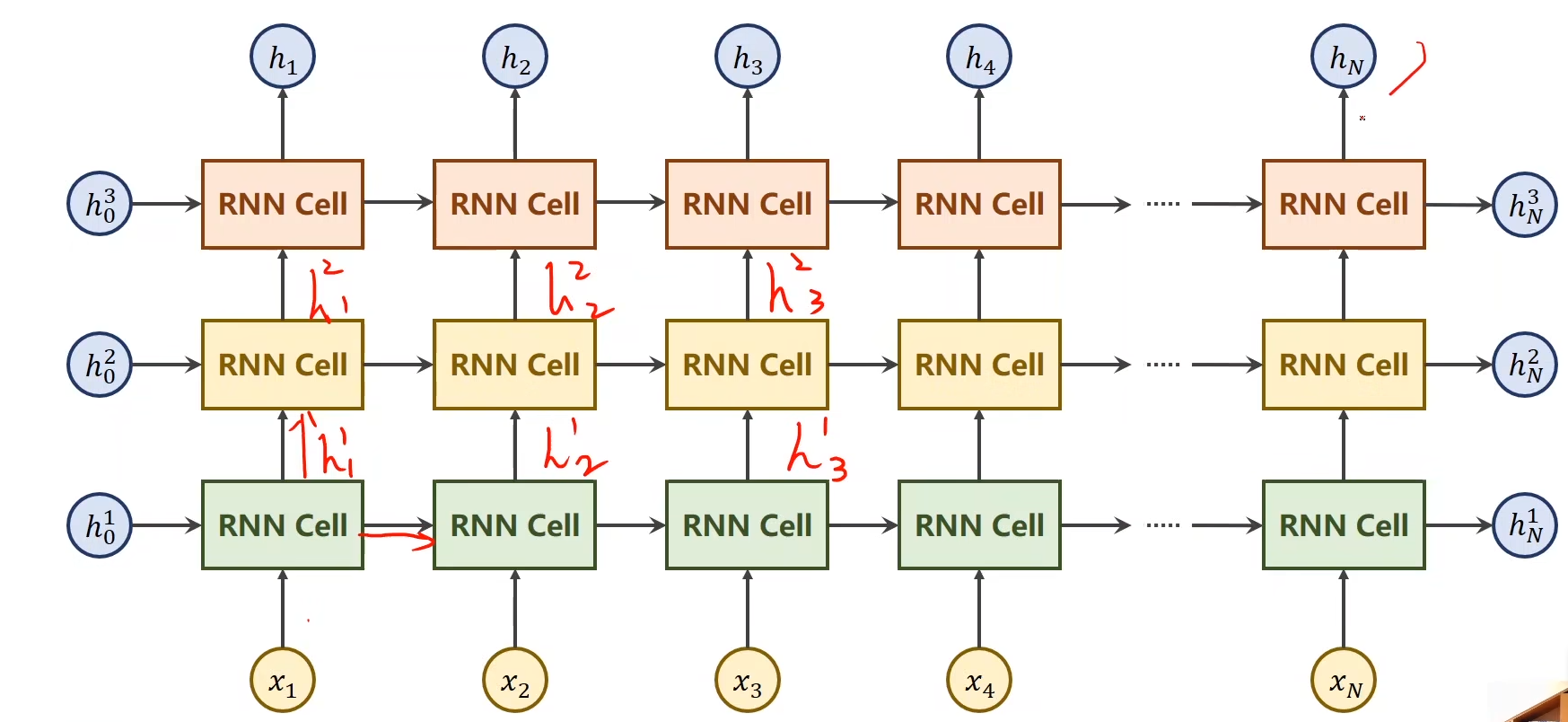
如图所示,我们可以将隐藏层加深。
图片看起来非常复杂,但实际上只有三个隐藏层,图中相同颜色的RNN CELL是同一个隐藏层。图中是将他展开之后的结果。
所以,左侧与下面是输入,右侧与上边的输出,每一个隐层最终都有一个输出,而每一个x也都有自己的一个输出。
torch.nn.RNN
通读官方文档

可以看到pytorch中的RNN是基于"Elman RNN"的除了,这种RNN,还有一种是叫做Jordan RNN,他俩的区别下:
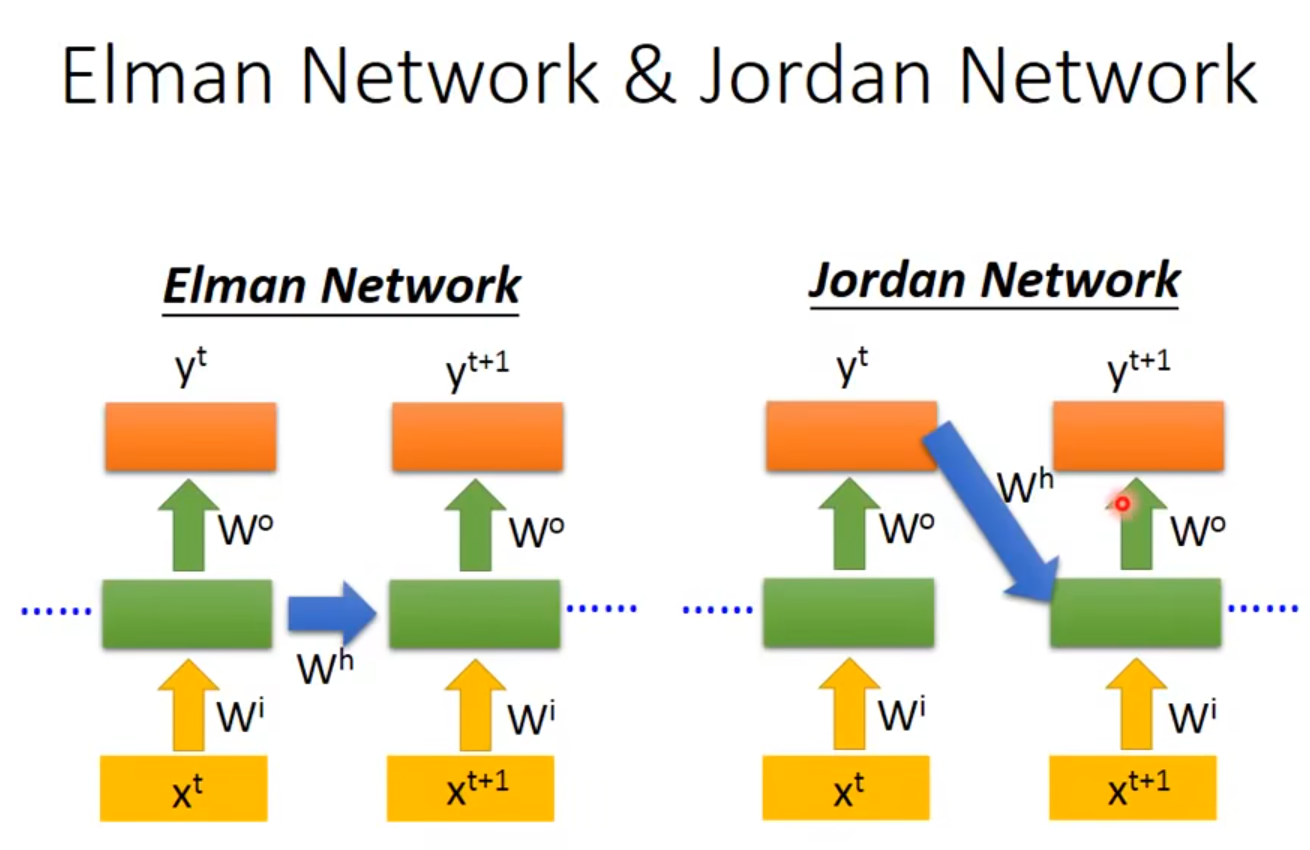
Jordan RNN的会将每一个最终输出的y值放到下一个时间点的之中,上边所讲的是Elman RNN的是将每一层的隐藏层的值放到下一个时间点。
因为Elman RNN的每一个循环层是相互独立的,因此网络结构的设计可以更加灵活,它不依赖于前一个输出值(有点像批量梯度下降和随机梯度下降的区别了。批量梯度下降是可以并行的)所以现在常用的RNN(包括LSTM、GRU等等)都是基于Elman network。所以现在提起RNN基本都指的是Elman RNN。
老样子,读一下第一句话,应用一个多层的Elman RNN with tanh或者RELU非线性函数 to 一个输入序列。对于每一个输入序列,每一层计算都依赖与以下函数。
实际上就是我们上边写的函数,只是人家这里把权重矩阵用两个下标表示,更为清晰。
第二句话
where is the hidden state at time , is the input at time ,and is the hidden state of the previous layer at time or the initial hidden state at time o.If nonlinearity is 'relu',then is used instead of .
所以之所以用t来当作下标,是表示时间,对于一个隐藏层,他是循环的执行上边那个公式,每一次循环对应一个time.
pytorch还贴心的写了一个对于上边那个公式的的实现,即forward函数
# Efficient implementation equivalent to the following with bidirectional=False
def forward(x, hx=None):
if batch_first:
x = x.transpose(0, 1)
seq_len, batch_size, _ = x.size()
if hx is None:
hx = torch.zeros(num_layers, batch_size, hidden_size)
h_t_minus_1 = hx
h_t = hx
output = []
for t in range(seq_len):
for layer in range(num_layers):
h_t[layer] = torch.tanh(
x[t] @ weight_ih[layer].T
+ bias_ih[layer]
+ h_t_minus_1[layer] @ weight_hh[layer].T
+ bias_hh[layer]
)
output.append(h_t[-1])
h_t_minus_1 = h_t
output = torch.stack(output)
if batch_first:
output = output.transpose(0, 1)
return output, h_t
接下来看一下torch.nn.RNN()的参数

input_size:每一个输入x向量的维度
hidden_size:隐藏层的维度.
num_layers:即上边"RNN CELL的DEEP用法"那一小结所讲,每一层的隐藏层是可以堆叠的,可以进行多层的线性计算 默认是1。
nonlinearity:即过程中,所涉及到的激活函数的选用,可以选择relu或者tanh,默认为tanh。
bias:即加不加偏执,默认加
batch_first:输入和输出维度原本是: (seq, batch, feature),将这个设置为true后,就会变为:(batch, seq, feature),关于这个输入输出,下文还会详细介绍
dropoutdropout一下
bidirectional:如果是true,即为双向循环神经网络
关于bidirectional
李宏毅老师这张图也是非常清楚
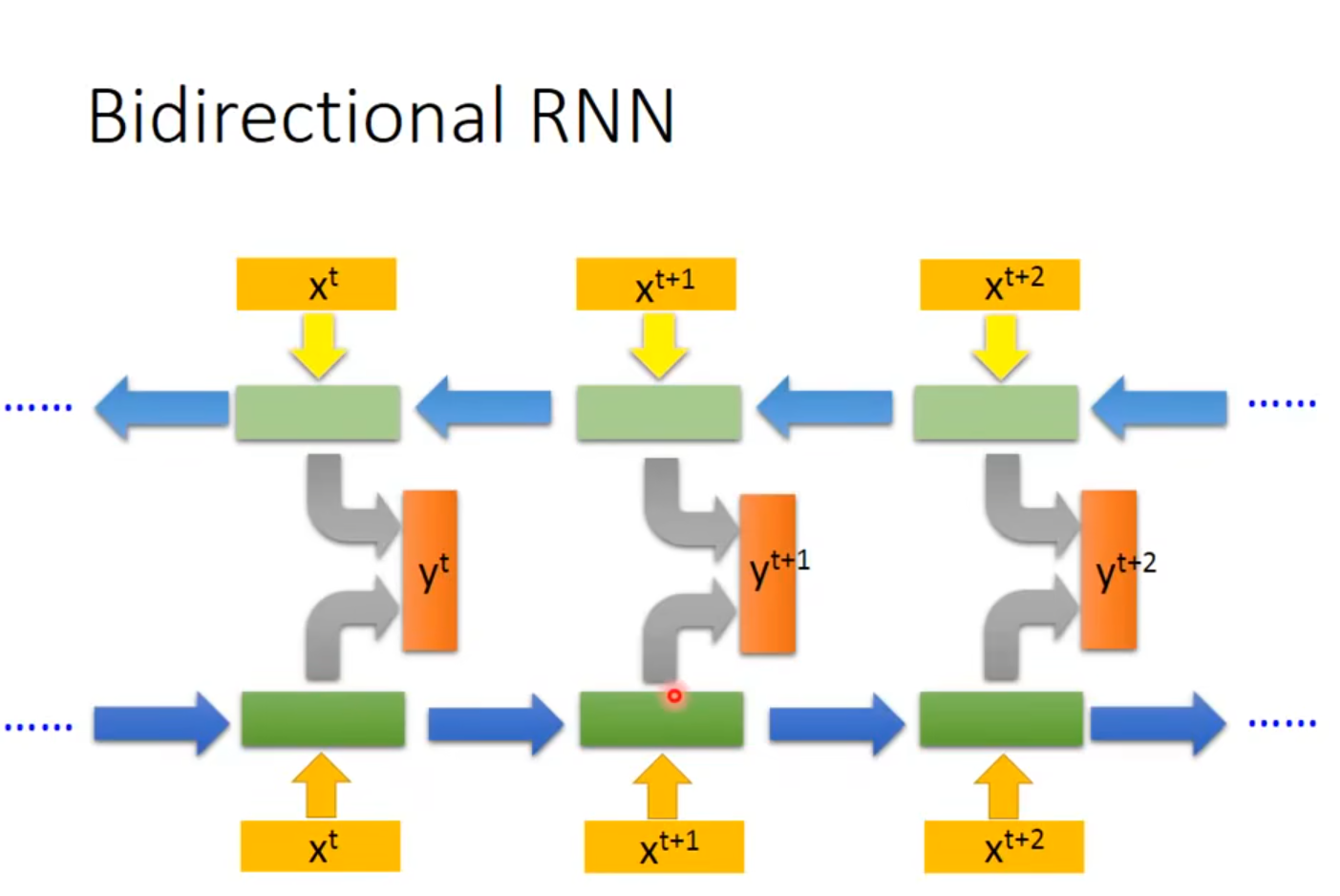
普通的RNN的hidden layer就只是正向的,从到,生成一个之后就直接讨一个线性变换就成为最终的输出y了,但是bidirectional会逆向的从到,生成一个,之后将这两个h一并进行线性变换,生成最终的输出。
RNN的输入输出

RNN的输入包含两部分,一个是输入的x,即input,另一个是输入的初始隐层,即
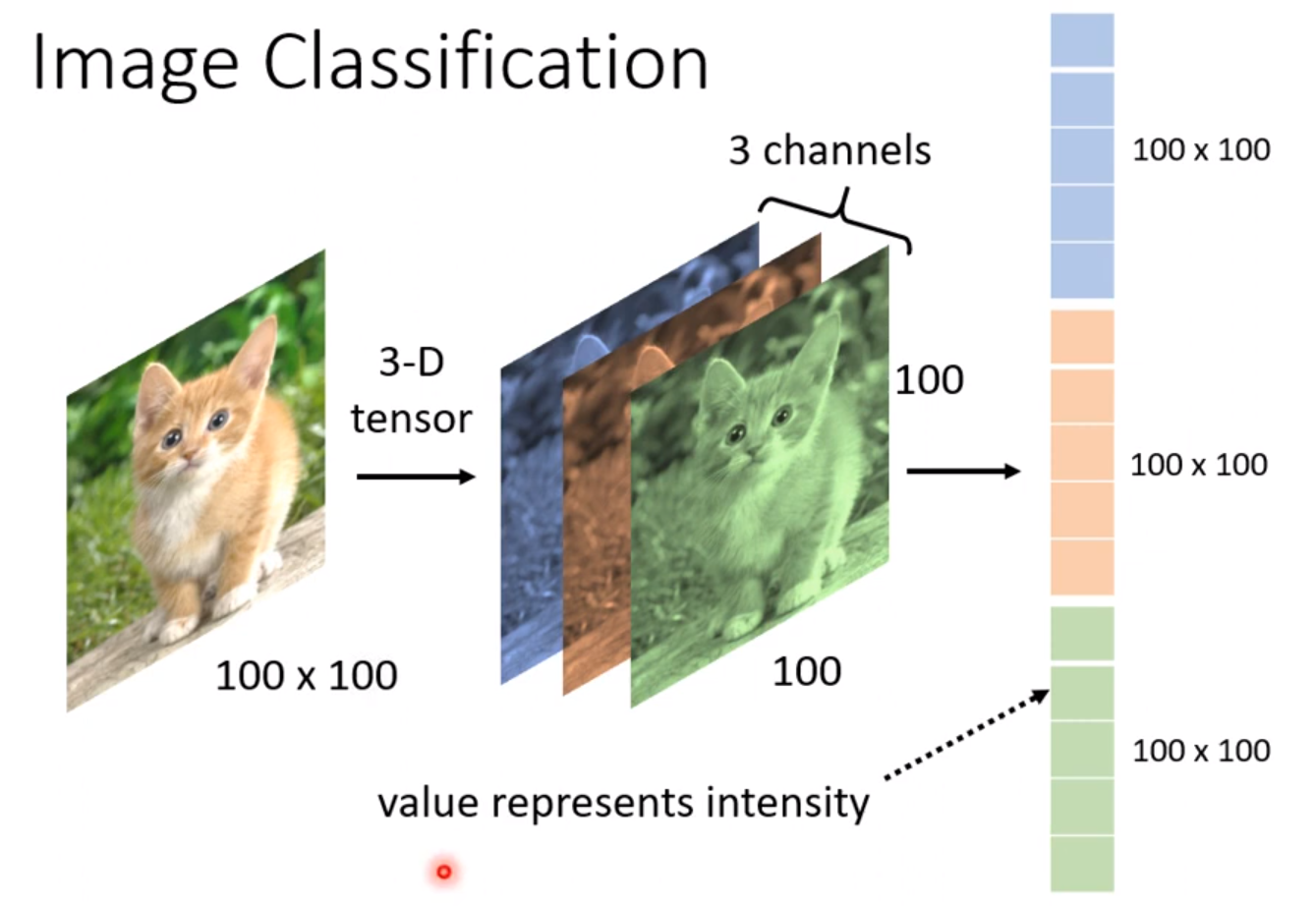
输入x是一个三维的向量:
(seq length,batch_size,input_ size)seq length:输入序列的长度,即输入序列转为向量,输入向量的个数batch_size:即batch_size.表示有多少个输入序列。input_size:即每一个输入向量的长度而h的输入维度是(D*num_layers,batch_size,hidden_size),如果是bidirectional,则D为2,如果是普通的RNN,则D为1

num_layers:num_layers是指h有多少层,如上图,num_layers为3。
batch_size:有多少个输入序列就有多少个输入的隐藏层,因为每输入一个序列,就会输入一个h。
hidden_size:输入的隐藏层h的维度。

而输出同样也包含两个部分,一个是输出的y,即output,另一个是隐藏层的输出。隐藏层输出的维度是和隐藏层输入的维度是完全一样的,但是输出的output却不太一样,输出的维度是·(sequence_length,batch_size,hidden_size),为什么?
因为在这个公式中
的是hidden_size×input_size大小的矩阵,然后是为inputsize×1的向量,这么一乘,每一个向量就成了hidden_size×1的向量,所以最终的维度就是hidden_size。
RNN的反向传播
上边介绍的都是RNN的forward,接下来想一下RNN的BP过程是什么样的?
RNN相比MLP和CNN的区别主要是,隐藏层多了一个循环结构,这个隐藏层是可以按照时间展开的,当前隐藏层不仅取决于,而且还取决于,是取决于上一时间的自己的。
所以RNN的反向传播叫做:Back-Propagation Through Time(BPTT)随时间反向传播
一个RNN的网络结构为:
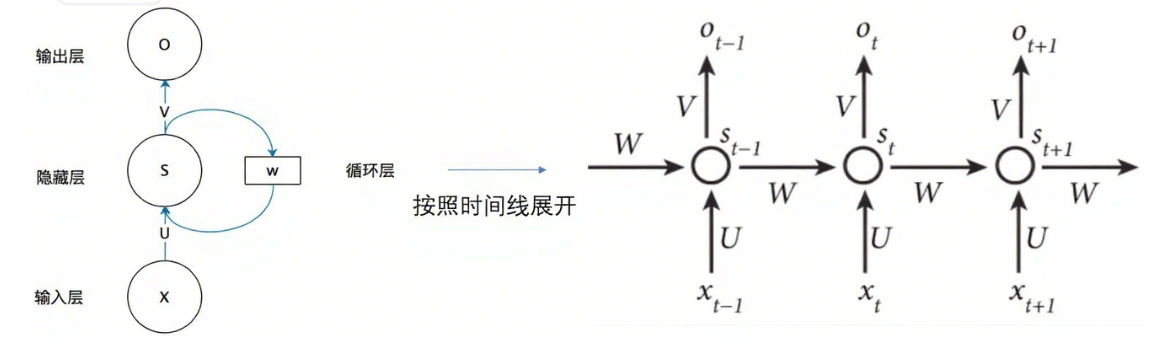
我们知道,如果只是一个普通的神经网络,那么我们会将输出的,也就是和实际上的通过损失函数计算损失值,然后通过反向传播,将损失值先对求偏导,之后层层反向传播,算出每一层的梯度,在这个过程中对将每一层的参数进行更新。
但是在RNN中,每一层隐藏层是可以通过时间展开的,并且每一时刻都会输出一个对应的,也就是说每一层的参数是附着于由不同时间段的以及的,并且对于该层,每一层的所有时刻都是权重共享的,,所以我们计算并更新梯度的时候,也要对每一时刻的参数进行梯度计算并更新。
RNN中的损失怎么计算?
我们知道,RNN擅长处理序列型数据,所以RNN和其他网络的不同之处是:他会在每一个时刻都输出一个值,对应每一个x,即:输入一个序列向量组,他会输出和这个序列向量个数相同的输出,来对应每一个向量,例如:
输入:[This, movie,is,great]
在将每一个单词转为向量后,生成一组向量,假设上边的词组利用onehot编码转为:
[[1 0 0 0][0 1 0 0][0 0 1 0][0 0 0 1]]
上边向量的维度是:(4,4),那么对于该序列,就是一共有4个输入x,并且每一个输入向量都是4维的。
那么RNN在正向传播的过程中,会对每一个输入向量都输出一个,也就是每一个时刻都会输出一个,那最终会输出4个,即,也就是上文中的。那损失该怎么计算呢?在其他网络中中,一般只会有一个输出,只需要将这个输出和实际的输出计算损失即可。但是RNN,他有多个输出,那这个时候怎么计算损失呢? 这个时候就需要考虑到底是什么任务类型了。当任务是序列到序列的任务时:例如文本翻译,那么我们就需要考虑每一个y,也就是对每一个时刻的y都计算损失,最后相加,即是整个神经网络的损失,但是如果问题是分类问题,例如文本分类、情感分类等,我们只需要对最后时刻的输出做损失即可,这个时候就不需要对每个时刻的y都求损失再相加。
但是无论是哪种任务,因为后一刻的h是由前一时刻的h决定的,那么就注定了我们在利用计算损失并进行梯度计算并更新的时候,一定会将前面的时刻都考虑进去。
这么说有点抽象
接下来以一个例子来说明RNN中在t时刻,对反向传播更新梯度的过程
RNN中反向传播推导过程
RNN的前向传播的过程为:
这里的三个权重矩阵也就是分别对应上图中的:U、V、W,接下来的推导过程是:t时刻的损失对三个权重的梯度计算的过程。
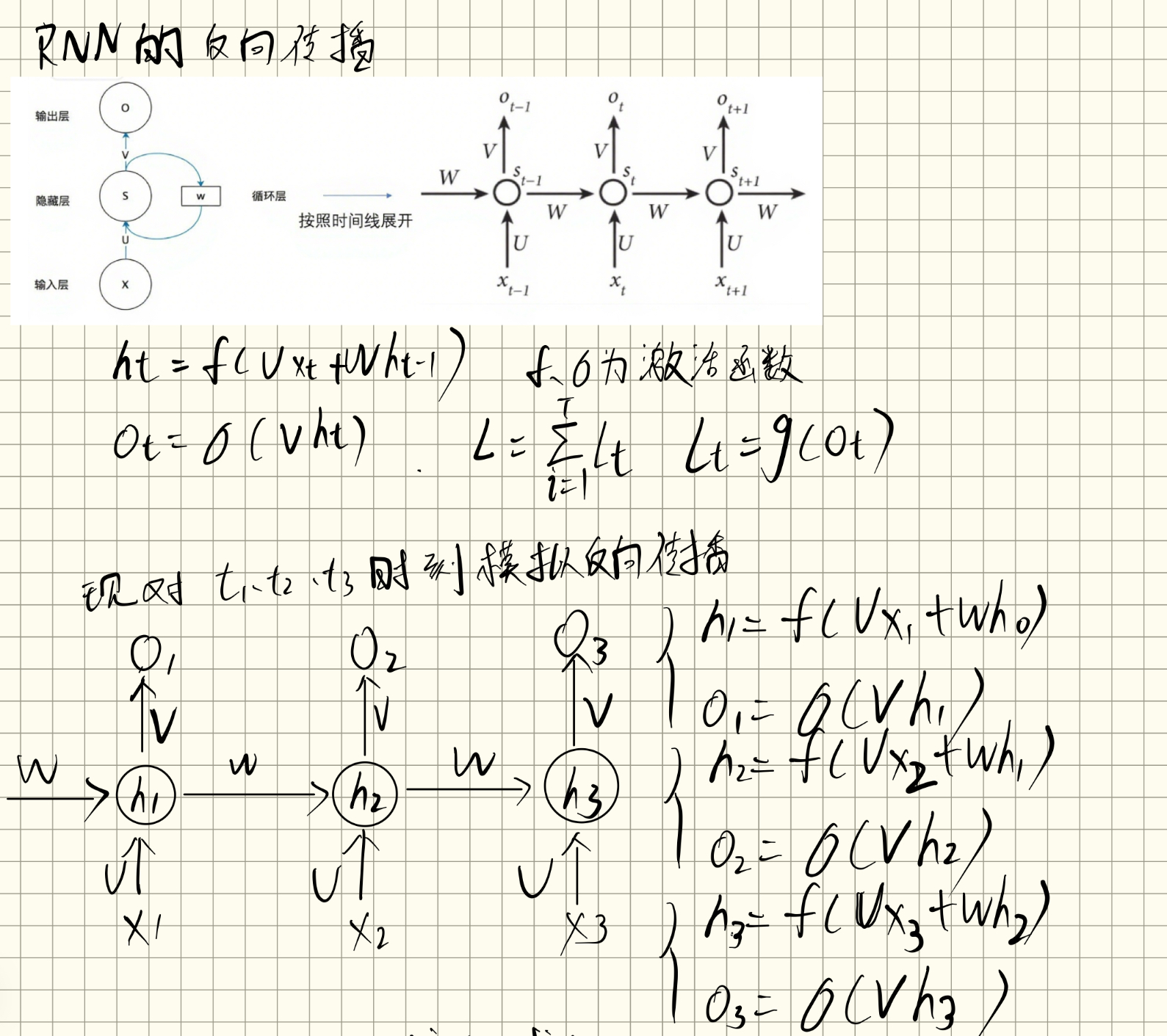


这样就得到了对三个参数的梯度计算公式。那梯度怎么更新,就是取决于什么任务了,如果是序列到序列的任务,那么就需要将每一个时刻的损失加起来。之后在反向传播的过程中进行梯度更新
如果是文本分类这样的任务,只需要将最后时刻的输出计算损失之后进行梯度更新即可。
小结
在我的理解中,RNN与MLP有一个最大的不同就是他会将序列中每一个x都产生一个输出,也就是不同时刻的输出,并且每一个时刻的x都包含了前面时刻x的信息,也就能更好的处理序列数据。