前言
之前也学习过反向传播,大概知道反向传播是为了更新权重,但是从来没想过一个问题,这个更新权重的行为的对象是什么?是一个样本?还是一批样本?这些都没想过,还有就是反向传播算法优化的是什么?在反向传播出现之前,都是怎么更新权重的? 这些也都没有想过,在本篇笔记中,这些问题都会提到并解决。
反向传播的意义
我们知道,反向传播算法是服务于神经网络的,那他为什么诞生?他优化的是什么? 接下来以一个简单的网络来举例子。
梯度下降简要介绍
在学习反向传播之前,首先要明白,我们是要通过这个网络来拟合一组样本数据,而这个拟合的方式就是构建一个损失函数,该损失函数应该符合:损失函数越小,最终拟合数据的结果越好。但是我们无法改变输入的x,只能改变里面的权重,那怎么修改权重才能更好呢?这个损失函数一般是由 (我们模型的预测输出值)和 (样本的实际输出值)决定的的一个函数式, 是已经知道的,而 是由我们的模型预测的,所以 肯定是由权重和x构成的一个函数式。那么该式子就可以对某个权重求偏导,这个结果就是该损失函数对于该权重方向上的的变化率,也就是该点在该方向上,下降或者上升最快的的方向(可以理解为最为陡峭的方向)。这个偏导数就可以看作这个方向上的梯度,那么就可以对这个权重进行一次更新
gradient就是这个方向上的梯度,在多元微分中,梯度的定义为:
对于一个有三个自变量的函数:
i, j, k 为标准的单位向量,分别指向 x, y 跟 z 坐标的方向。
为该函数的梯度。而当前位置的梯度方向,就是函数值上升最快的方向,反方向为下降最快的方向。
可以看到一个函数的梯度是所有自变量方向上的梯度的代数和。所以我们在梯度更新的时候,可以对每个权重分别更新,在全部权重更新之后,这个函数也就沿着下降最快的方向下降了一段距离。
那学习率的作用是什么?虽然沿着梯度下降是最快的方向,但是这个步伐无法控制,学习率就是用来控制步伐的,我们的目的是到达最低点,即让损失函数达到最小,但是如果步伐太大可能就会越过最小值的地方,就达不到最小值了。所以通过学习率,我们可以每次以一个小步伐向着最小的方向下降,并且循环。那到底循环多少次呢?这就是平时训练时提到的一个概念:epoch。我们无法判断到底循环多少次才能走到最低点,所以一般就控制一个轮数,这个数就叫epoch
为什么要反向传播?
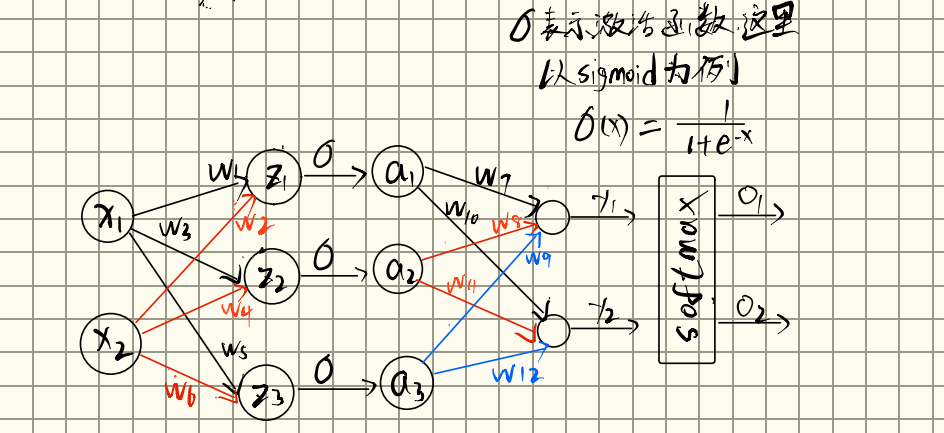
现在我们知道了,要想优化损失函数,进行权重更新,那么就需要知道,那么就需要从输入开始,走一遍我们的模型,得到我们的输出 .再通过 和 计算每个权重的梯度,并分别进行更新。那走一遍我们模型的这个过程就叫做前向传播。就像这样子:
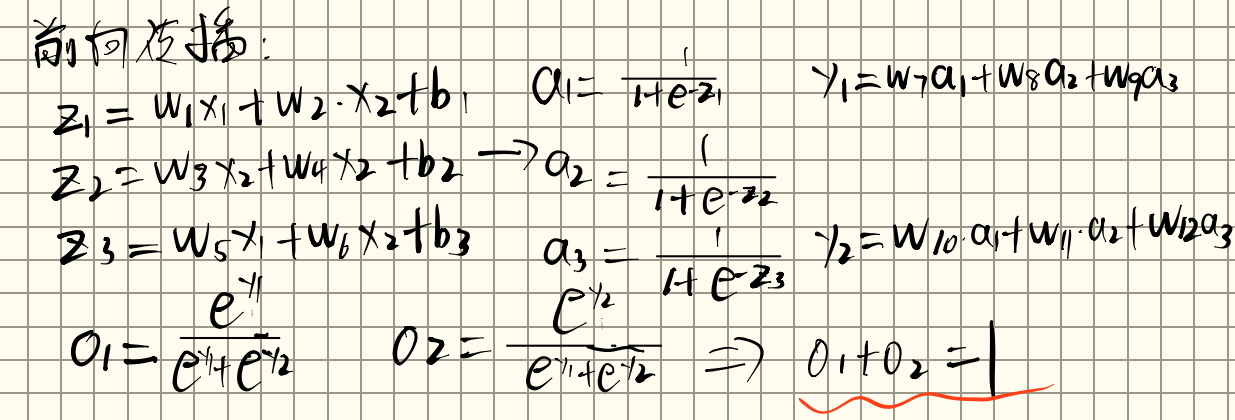
我们得到了两个输出,现在要根据损失函数更新我们的权重
因为最终是softmax输出,所以规定损失函数为:
其中为真实标签值,为预测值,默认log以e为底等于ln
这里有两个输出,所以
loss为:
我们要更新的参数有
现在对求偏导为例:
根据链式法则:

最终可以得到:

这个式子里的各项都是可以计算的,同理 对于其他权重,我们也都可以列出来这样一个求偏导的式子,然后一个一个都算出来,并且更新。
这样做有什么问题? 我们发现,很多式子都是会重复计算的,例如上边的例子,在求的过程中,就顺便将给求出来了,但是真到求这两个权重的时候,我们又得重新求。这就造成了资源的浪费。我们发现,上一层是依赖于下一层的,所以我们可以想到:那直接从输出反着走一遍网络,顺便更新参数,并且将每个偏导值(梯度)给暂存起来,那只需要一边正向传播,一遍反向传播,我们就可以对每个权重完成更新,这就是反向传播算法。
反向传播的过程
反向传播的前提是前向传播:
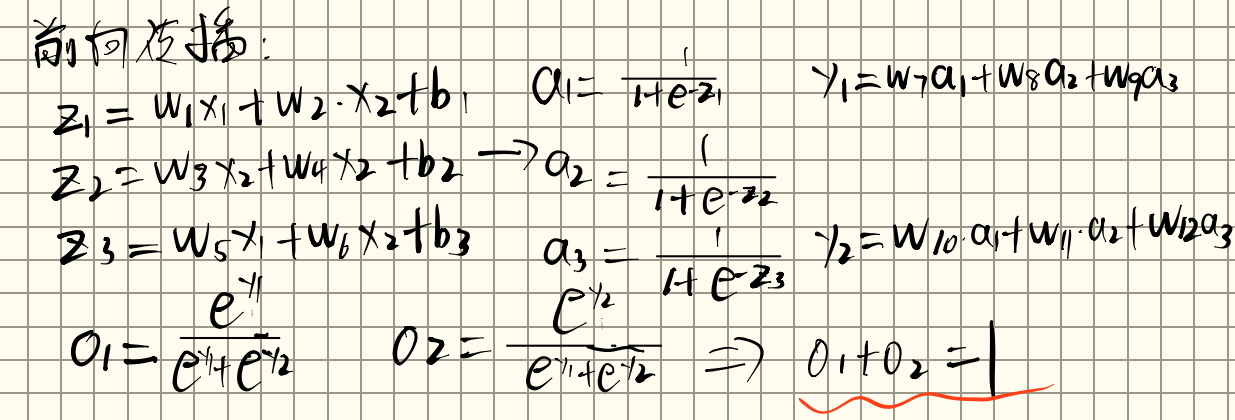
损失函数为:
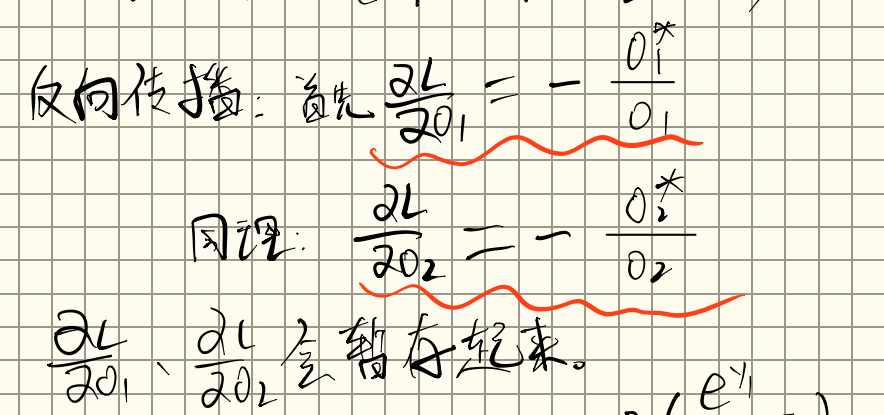
接着进行反向传播:
首先先算损失对两个输出的偏导数
接着继续反向传播,计算对的偏导

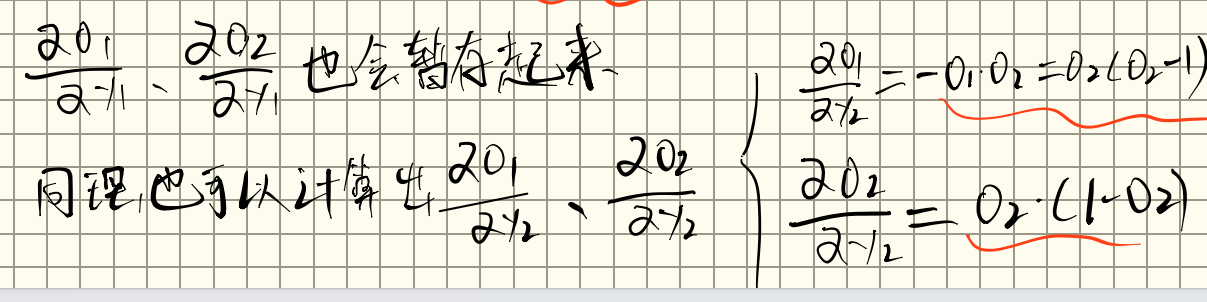
接着继续传播,终于传播到了权重

我们发现损失对的偏导所需要的式子,在反向传播的过程中都缓存了起来,直接将缓存的值代入即可
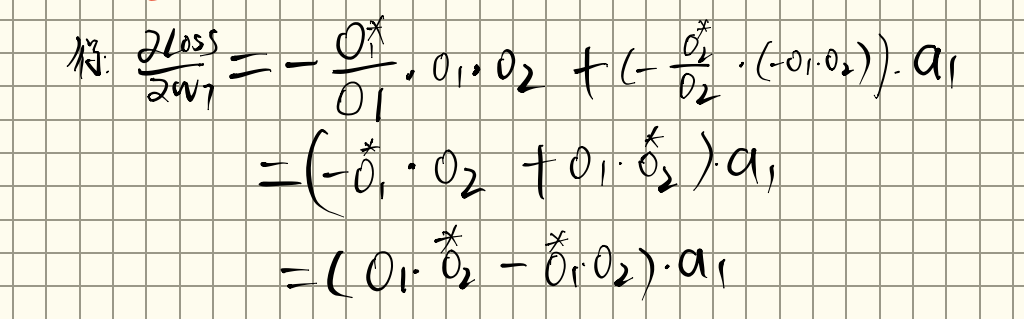
然后对进行权重更新(梯度下降)
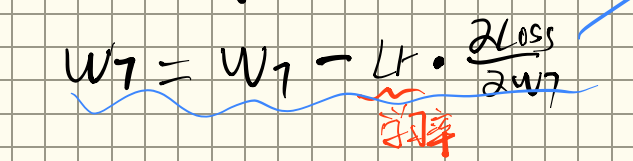
同理,对于其他权重,都是一样的道理,在反向传播的过程中,在到达该权重时,计算该参数的梯度所需要的值,都已经在反向传播的过程中缓存好了,只需要代入计算即可,这样,经过一次正向传播+反向传播,我们就可以对网络中的所有参数进行一次更新。之后,只要不断循环,更新数个epoch,就会趋向收敛,损失函数趋向最小。
批量梯度下降与小批量梯度下降
上边反向传播更新权重的过程,仅仅是针对一个样本来说的。仅仅通过一个样本,来更新所有权重,显然是不科学的,所以想要达到拟合整个数据集,我们需要对所有样本都进行上边的反向传播,并且每次对权重的更新取整个样本对该权重更新的平均值(可以每个样本并行运算,之后取平均值更新权重),这样经历若干的epoch之后,得到的就是全局最优下降梯度。这个方法叫做批量梯度下降。
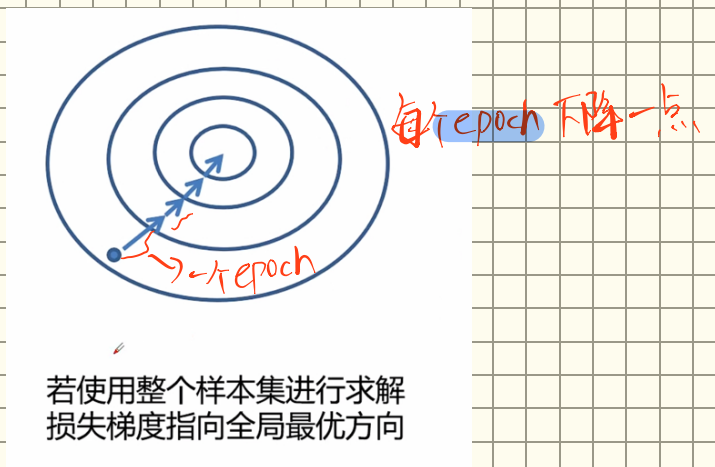
但实际训练中,当数据集过大时,我们无法对整个数据集进行权重更新,一个原因是内存不够,第二就是计算的太慢了,所以我们会将数据集分成若干份。每一份就是一个batch,我们会对每个batch中的数据进行综合考虑更新权重,这样下降的速度会快很多。但是,这样也有缺陷,因为每个batch没有考虑所有的数据,所以下降的方向是不一定趋向于最终的最小值的。
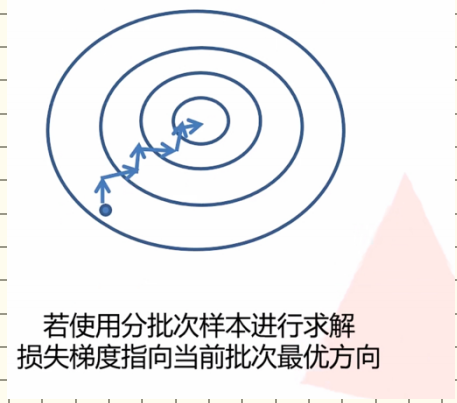
可以看到下降的过程不是很平稳,并且可能陷入局部最优解无法跳出,所以因为这个问题,就引出了很多的方法来优化,即优化器(optimazer),上边的方法叫做SGD(随机梯度下降),是优化器的一种,为了优化各种问题,就诞生出许许多多的优化器,如adam等。
关于各种优化器,就等到遇到了再具体进行学习吧。