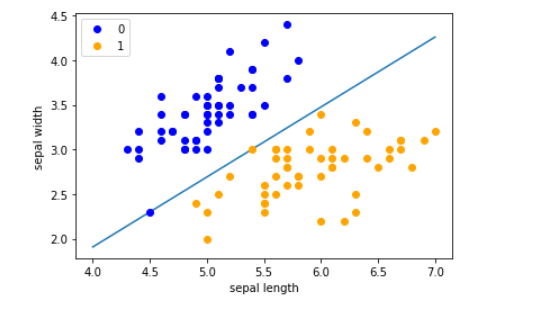
什么是K近邻
k近邻算法就和他的名字一样浅显易懂: K Nearest Neighbors:k个最近的邻居。在生活中我们也常用这种方法来判断一个东西的好坏,用于分类。"近朱者赤,近墨者黑"这一句就有KNN的原理。
在机器学习中,knn实际上就是利用训练集对特征向量空间进行划分,对于测试集的每个点,找到该点所在的区域,找到离他最近的k个点,如果是分类问题,一般选择多数表决法,也就是遵从少数服从多数的原则,如果是回归问题,那就是取这k个点的平均值作为输出,本文章只对分类问题进行阐述。
K近邻的三个要素
- 分类决策规则:分类决策规则一般采用上边提到的分类表决法
- 距离度量:对于度量两个点的距离的方式,一般采用欧式距离,欧式距离在高中就应用过:例如求两个点$(x_1,x_2),(y_1,y_2)$的距离:
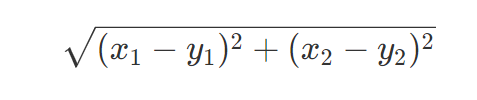
这是二维的,当上升为多维:即对于两个n维向量x和y
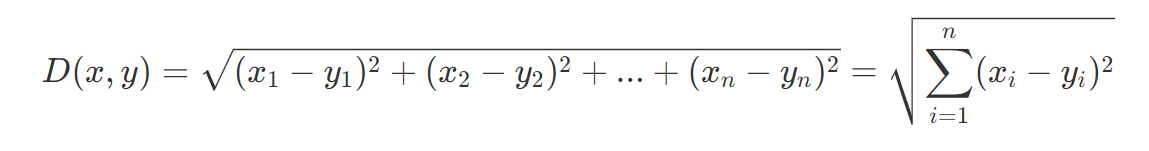
除了欧式距离,也可以使用其他距离,如曼哈顿距离。
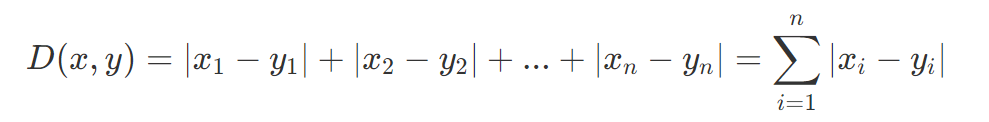
不管是欧式距离,还是曼哈顿距离,都来源于:闵可夫斯基距离(Minkowski Distance):

欧式距离是p=2的情况,曼哈顿距离为p=1的情况。
- k值的选择:
k值没有一个固定的选择,一般都是根据数据集来调整,可以使用交叉验证来选择合适的k值- 当k值过小,误差会减小,只有与输入点相聚很近的点才会影响结果,整个模型会变复杂,会导致过拟合。
- 当k值过大,会增加训练误差,但是会减少泛化误差(减少过拟合),但是会导致模型过于简单,举个极端的例子,当k=样本数,这时候,不管输入什么,都是一个输出,就是样本中最多的那一类,这样是不可取的
一般k值采用交叉验证的方法来选取最优的k值
- 关于交叉验证的例子:
- 数据准备:将数据集分为两个部分,一个是用于训练的训练集,另一个是用于交叉验证的验证集。通常,你可以使用 70% - 80% 的数据作为训练集,剩余的作为验证集。
- 选择 k 值的范围:确定 k 值的候选范围,例如从 1 到 20,或者根据你的问题领域经验进行选择。
- K 折交叉验证:将训练集分成 k 个子集,其中一个子集用作验证集,其余子集用作训练集。然后,重复以下步骤 k 次,每次选择不同的验证集:
- 使用训练集来训练 KNN 模型,使用不同的 k 值(在候选范围内)。
- 使用验证集来评估模型性能,通常使用分类准确率、F1 分数、均方误差等指标来度量
- 性能评估:对于每个 k 值,计算 k 次验证的性能指标的平均值。这将为每个 k 值提供一个性能估计。
- 选择最佳 k 值:根据性能指标的平均值,选择性能最好的 k 值。通常,较佳的 k 值是能够提供较高性能的值。
k近邻的实现
暴力实现(线性扫描)
因为我们要找到距离测试集点的最近距离的k个点,那暴力方法就是算出训练集中的每个点到该点的距离,然后找到最近的k个点就可以了。这种方法简单直接,适用于数据集较少的情况下,当数据集较大的时候,这种方法就不太适合了。
kd树实现
定义:kd树是一种对k维空间中的样本点进行存储以进行快速检索的树形数据结构,这里的k指的是k维样本点,而不是上文中k近邻中的k,构造kd树就是不断的用垂直于坐标轴的超平面将k维空间切分,构成一系列的k维超矩形区域
构建kd树的过程:所谓kd树,本质上是一颗二叉树,根节点为某一维度的中位数(最靠近中位数的点),该点将其他点划分为两个区域,过该点做垂直于该维度的一个超平面,这个平面的左边的点为一个区域,右边的点为一个区域,在左区域下,以下一个维度作为划分维度,取该维度下最靠近当前维度的中位数那个点,继续划分区域,右边区域也一样,划分的两个区域没有样本点时,停止。
还是很抽象,接下来以一个实际例子来说明kd树的构建过程。
例:
给定一个二维空间的数据集:
$$T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}$$
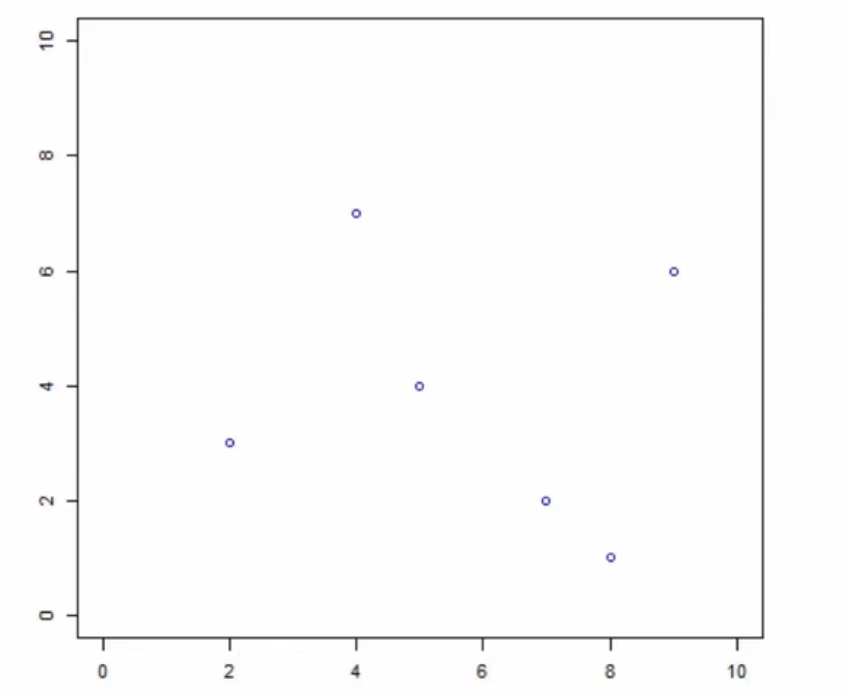
- 根节点需要确定一个维度,我们一般选取方差较大的哪个维度作为根节点的维度,第一维度为:{2,5,9,4,8,7}。他们的方差为6.97,第二维度:{3,4,6,7,1,2}。第2维度方差为5.37。我们选取第一维度作为确定根节点的维度。下面统称第一维度为x维度,第二维度为y维度,
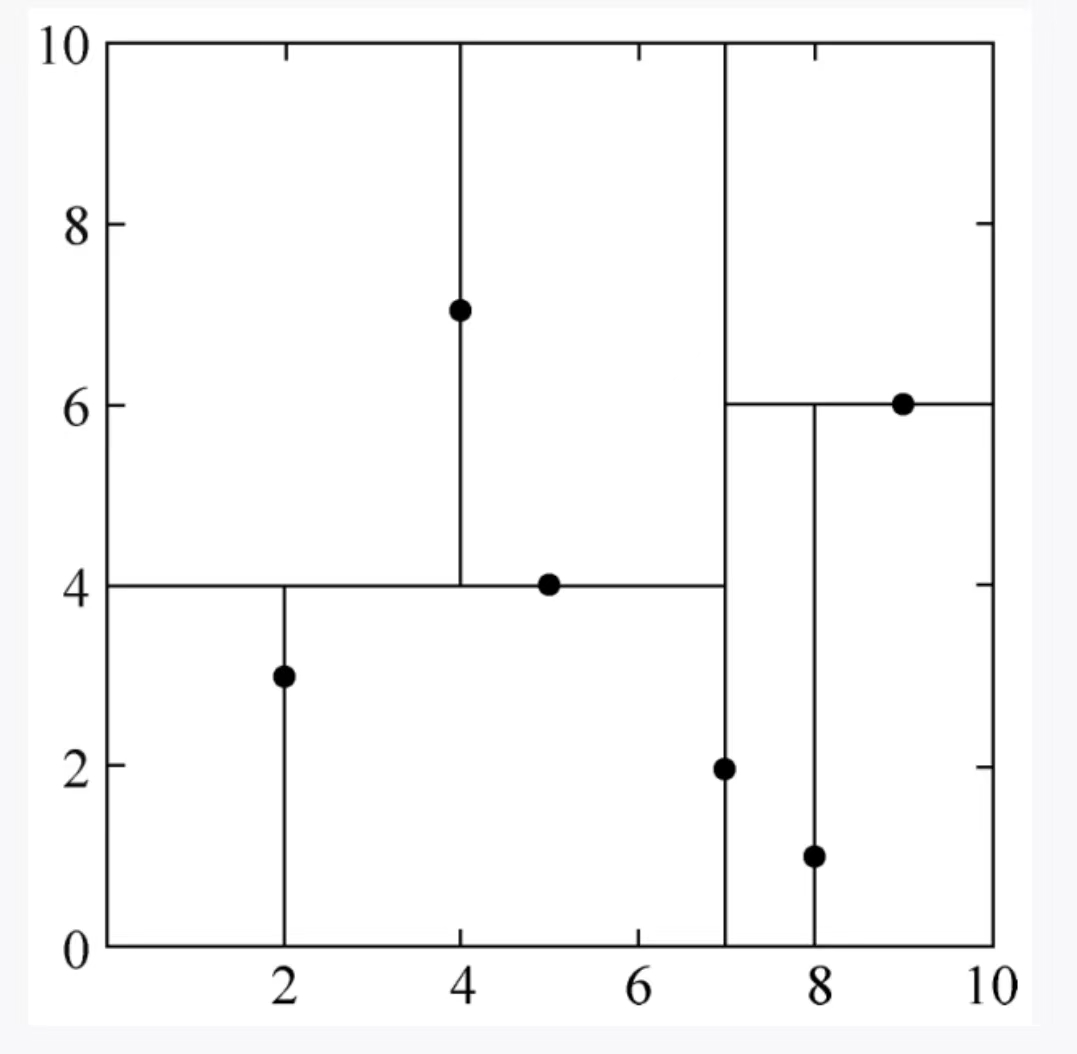
- 找到x维度的最靠近中位数的一个点,x维度排一下序为{2,4,5,7,8,9}中位数为6,我们选择5或者7都可以,这里我们选择7,那根节点就是(7,2)这个点。然后通过该点分割超平面,因为该点是x维的,所以过该点,做y维的垂线,将平面分为两个区域,在该区域左边的x坐标为:2,4,5。对应的点为:(2,3)(4,7)(5,4),而右边的区域x坐标为8,9。对应的坐标为:(8,1)(9,6)
- 接着,看左边区域:有(2,3)(4,7)(5,4)三个点这时候再划分就不能做x轴的垂线划分了,要以下一个维度作为划分,这时候三个点的y坐标分别为:3,7,4,中位数为4,那就是以(5,4)这个点划分,做垂线。
- 同理,右边区域也一样,以此类推,直到划分的左右区域内没有样本点。
得到:
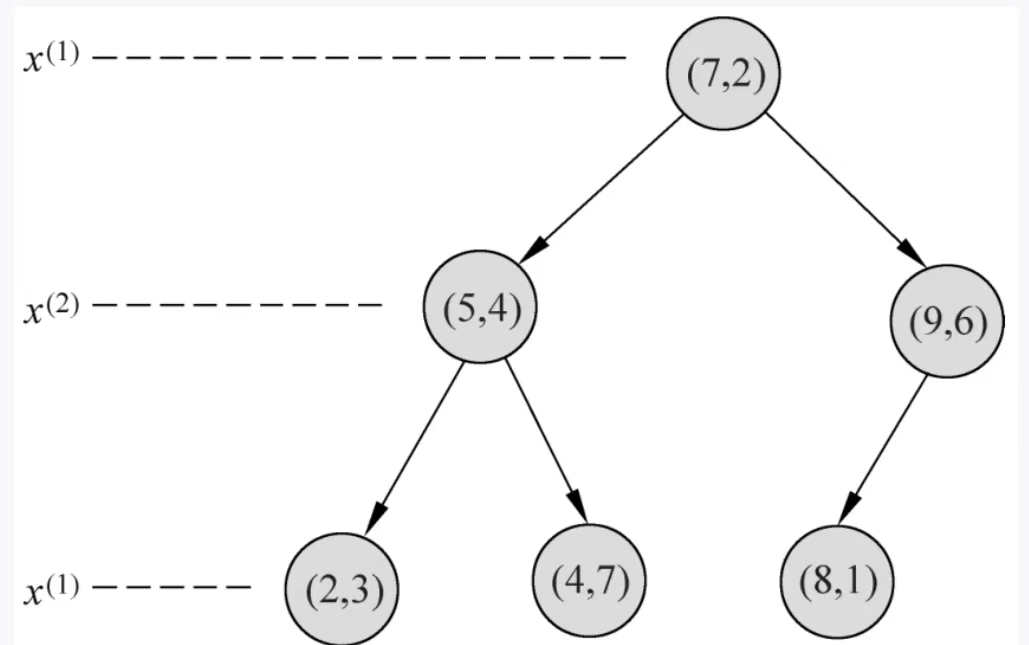
得到的kd树为:
汇总一下构造kd树的过程为:
搜索kd树
搜索的过程可以简单分为以下几步:
- 寻找当前最近点:根据kd树划分的方法,从根节点出发,分别判断目标点在当前层所划分的维度的哪个区域,直到划分到一个叶子节点的某一区域,此时该叶子节点为当前最近点,以目标点为圆心,目标点与当前最近点的距离为半径绘制一个超球体,最近的相邻点一定在这个球体内部。
- 回溯:从当前最近点开始回溯,返回当前最近点的父节点,判断父节点所在的超平面与这个超球体是否相交,如果相交,那么就要计算一下该父节点的另一个子节点(如果另一个子节点是空的,那就直接回溯)和目标点的距离,如果该距离小于当前最近点的与目标点之间的距离,那么就更新当前最近点。之后往上回溯,返回父节点的父节点,如果不相交,那就直接往上回溯,返回父节点的父节点,继续判断。
- 直到回溯到根节点。判断一下此时保存的当前最近点就是目标点最终的最近邻。
例:
输入:kd树,目标点x=(2.4,5)
这里我们使用上边构造好的kd树来用 - 首先从根节点(7,2)出发,2.4在7的左子区域,所以向下走,到(5,4)这个点,这个维度是以y维划分的,5在2的右子区域,所以往下走,到(4,7)这个点,接着,以x维划分,2.4在4的左侧,此时再往下没有点了,所以我们划分完毕,当前最近点就为(4,7)
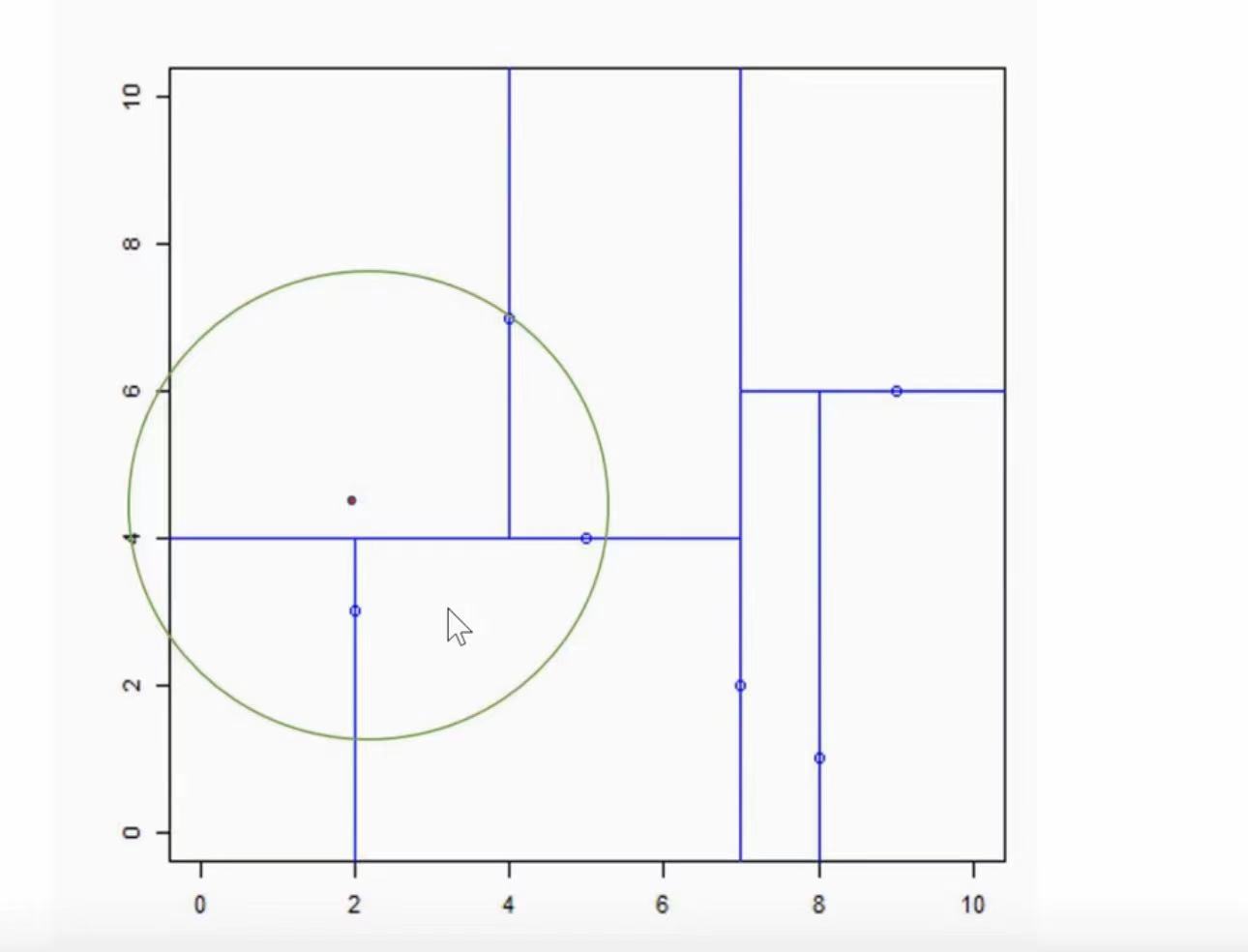
- 以(2.4,5)为圆心,(2.4,5)与当前最近点(4,7)的距离为半径做一个超球体(这里是二维,所以为一个圆)
- 接着回溯,往上走到(4,7)的父节点(5,4),如图所示,(5,4)所在的这个平面(这里是二维,那就是一条线)与该圆相交,所以我们计算(5,4)的另一个子节点(2,3)与目标点的距离,通过计算得出(2,3)与目标点(2.4,5)的距离比当前最近点(4,7)与目标点(2.4,5)的距离小,所以我们这里更新当前最近点为(2,3)
- 然后继续向上回溯到(7,2),该点所在的超平面(直线与)超球体(圆)没有交集,并且已经到了根节点,已经无法回溯了。所以我们这里记录当前最近点(2,3)为目标点(2.4,5)的最近点。
总结补充
这里是用的书上的例子,比较简单,但是实际上还有很多情况,这里只举例出了一次性找最近的一个点的方法,在实际中是可以办到一次性找最近的k个点的。还有就是父节点的子节点还有子节点的情况,书中都没有举例。我网上找到了一篇比较详细文章:
https://www.joinquant.com/view/community/detail/c2c41c79657cebf8cd871b44ce4f5d97
知乎地址:
https://zhuanlan.zhihu.com/p/23966698