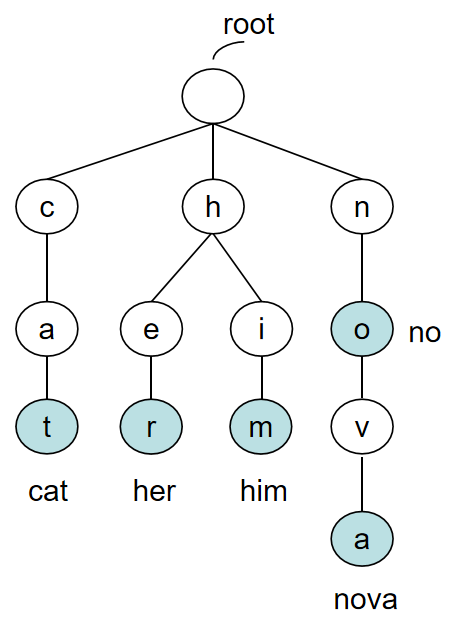
1链表
链表很简单,但是用数组模拟起来是真烦人,也可能我昨天脑子抽抽了。被各种没脑子的bug卡很久。。。
单链表
数组模拟链表:
所用的变量
//
struct node
{
int val;
int next;
} a[10000000];
int idx; // 当前数组用到的下标,可以理解成没有用的新地址。
int head;//头结点的地址初始化:
head = -1; // 让头结点指向空
idx = 0;头插:
void input_head(int num)
{
这里是让新的节点作为头结点,而不是插到头结点的后边。
a[idx].next = head;
a[idx].val = num;
head = idx;
idx++;//这个地址用过了,所以要++。
}因为链表本身的查找效率低,所以当要在某个点后边插入值或者在删除某个点,都要找到他再进行接下来的操作。但是当要求是,删除插入的第k个点后边的点,或者在插入的第k个点之后插入某个值的时候,这时候就比较简单,因为我们用的地址都是记录过的idx
idx从0开始,所以第k个数的下标为k-1。
在下标为k的节点后边插入num
void input_k(int k, int num)
{
a[idx].val = num;
a[idx].next = a[k].next;
a[k].next = idx;
idx++;
}删除下标为k的后边那个节点
void dele(int k)
{
a[k].next = a[a[k].next].next;
}遍历
没什么好说的,让一个指针指向头结点,然后一直往后就ok
int i = head;
while (i != -1)
{
printf("%d ",a[i].val);
i = a[i].next;
}题目:
实现一个单链表,链表初始为空,支持三种操作:
1 向链表头插入一个数;
2删除第 k个插入的数后面的数;
3在第k个插入的数后插入一个数。
现在要对该链表进行M次操作,进行完所有操作后,从头到尾输出整个链表。
注意:题目中第 k个插入的数并不是指当前链表的第 k个数。操作过程中一共插入了 n个数,则按照插入的时间顺序,这 n个数依次为:第 1个插入的数,第 2个插入的数,…第 n个插入的数。
输入格式第一行包含整数 M,表示操作次数。接下来 M行,每行包含一个操作命令,操作命令可能为以下几种:
H x,表示向链表头插入一个数 x。
D k,表示删除第 k个插入的数后面的数(当 k为 0时,表示删除头结点)。
I k x,表示在第 k个插入的数后面插入一个数 x(此操作中 k均大于 0)。
输出格式
共一行,将整个链表从头到尾输出。
数据范围
1≤M≤100000
所有操作保证合法。
输入样例:
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6
输出样例:
6 4 6 5
AC代码:
#include <bits/stdc++.h>
using namespace std;
struct node
{
int val;
int next;
} a[10000000];
int idx; // 当前数组用到的下标
int head;
void input_head(int num)
{
a[idx].next = head;
a[idx].val = num;
head = idx;
idx++;
}
void input_k(int k, int num)
{
a[idx].val = num;
a[idx].next = a[k].next;
a[k].next = idx;
idx++;
}
void dele(int k)
{
a[k].next = a[a[k].next].next;
}
int main()
{
// 初始化
head = -1; // 让头结点指向空
idx = 0;
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
char x;
cin >> x;
if (x == 'H')
{
int num;
scanf("%d", &num);
input_head(num);
}
if (x == 'I')
{
int num, k;
cin >> k >> num;
input_k(k - 1,num);
}
if (x == 'D')
{
int k;
cin >> k;
if (k == 0)
head = a[head].next;
else
dele(k - 1);
}
}
int i = head;
while (i != -1)
{
// printf("%d %d %d\n", idx, a[i].val, a[i].next);
printf("%d ",a[i].val);
i = a[i].next;
}
return 0;
}双链表
在单链表的基础上加了一指向前一个节点的指针,所以最开始要初始化两个端点,并且不存数据
题目:
实现一个双链表,双链表初始为空,支持 5种操作:
在最左侧插入一个数;
在最右侧插入一个数;
将第 k个插入的数删除;
在第 k个插入的数左侧插入一个数;
在第 k个插入的数右侧插入一个数
现在要对该链表进行 M次操作,进行完所有操作后,从左到右输出整个链表。
注意:题目中第 k个插入的数并不是指当前链表的第 k个数。例如操作过程中一共插入了 n个数,则按照插入的时间顺序,这 n个数依次为:第 1个插入的数,第 2个插入的数,…第 n个插入的数。
输入格式
第一行包含整数 M,表示操作次数。
接下来 M行,每行包含一个操作命令,操作命令可能为以下几种:
L x,表示在链表的最左端插入数 x
R x,表示在链表的最右端插入数 x
D k,表示将第 k个插入的数删除。
IL k x,表示在第 k个插入的数左侧插入一个数。
IR k x,表示在第 k个插入的数右侧插入一个数。
输出格式
共一行,将整个链表从左到右输出。
数据范围
1≤M≤100000
所有操作保证合法。
输入样例:
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2
输出样例:
8 7 7 3 2 9
#include <bits/stdc++.h>
using namespace std;
struct node
{
int val;
int l;
int r;
} a[10000000];
int idx; // 当前数组用到的下标
void input(int k, int num) // 在索引为k右边的插入num,如果要实现向k的左边插入,那就是在索引为k-1的右边插入
{
a[idx].val = num;
a[idx].l = k;//新节点的左边指向k的地址
a[idx].r = a[k].r;//新节点的右边指向k的下一个
a[a[k].r].l=idx;//第k个节点的下一个左指针指向新节点
a[k].r = idx;//第k个节点的右边指向新节点
idx++;
}
void dele(int k)
{
a[a[k].l].r = a[k].r;
a[a[k].r].l = a[k].l;
}
int main()
{
// 初始化
// 这里的a[0]和a[1]就相当于两个端点,是不存数据的
a[0].r = 1;
a[1].l = 0;
idx = 2;
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
string x;
cin >> x;
if (x == "L")
{
int num;
cin >> num;
input(0, num);
}
else if (x == "R")
{
int num;
cin >> num;
input(a[1].l, num);
}
else if (x == "D")
{
int k;
cin >> k;
dele(k + 1);
}
else if (x == "IL")
{
int k, x;
cin >> k >> x;
input(a[k + 1].l, x);
}
else if (x == "IR")
{
int k, x;
cin >> k >> x;
input(k + 1, x);
}
}
int i = a[0].r;
while (i != 1)
{
printf("%d ", a[i].val);
i = a[i].r;
}
return 0;
}栈
很简单
模拟栈
int sk[1000000];
int top=-1;
void push(int x)//入栈
{
sk[++top]=x;
}
void pop()//弹出
{
top--;
}
bool empty()//判断是否为空
{
if(top==-1)return true;
return false;
}
int querey()//返回栈顶元素
{
return sk[top];
}例题
给定一个表达式,其中运算符仅包含 +,-,,/(加 减 乘 除),可能包含括号,请你求出表达式的最终值。
注意:
数据保证给定的表达式合法。
题目保证符号 - 只作为减号出现,不会作为负号出现,例如,-1+2,(2+2)(-(1+1)+2) 之类表达式均不会出现。
题目保证表达式中所有数字均为正整数。
题目保证表达式在中间计算过程以及结果中,均不超过 231−1。
题目中的整除是指向 0取整,也就是说对于大于 0的结果向下取整,例如 5/3=1对于小于 0的结果向上取整,例如 5/(1−4)=−1。
C++和Java中的整除默认是向零取整;Python中的整除//默认向下取整,因此Python的eval()函数中的整除也是向下取整,在本题中不能直接使用。
输入格式
共一行,为给定表达式。
输出格式
共一行,为表达式的结果。
数据范围
表达式的长度不超过 105
。
输入样例:
(2+2)*(1+1)
输出样例:
8
还没写。留个坑。
我是坑 单调栈
单调栈就是让栈内元素满足单调性:
单调递减栈:检查一下新入栈的元素,如果比栈顶元素大,就弹出这个栈顶元素,一直弹到栈顶元素比新入栈的元素大或者栈为空,然后将这个元素入栈。
反之亦然。
例题
给定一个长度为 N的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 −1
。
输入格式第一行包含整数 N,表示数列长度。
第二行包含 N 个整数,表示整数数列。
输出格式共一行,包含 N个整数,其中第 i个数表示第 i个数的左边第一个比它小的数,如果不存在则输出 −1。
数据范围
1≤N≤105
1≤数列中元素≤109
输入样例:
5
3 4 2 7 5
输出样例:
-1 3 -1 2 2
首先想一下暴力做法。
for(int i=0;i<n;i++)
{
for(int j=i-1;j>=0;j--)
{
if(a[j]<a[i])
{
minans=a[j];
break;
}
}
if(minans<a[j])cout<<manans
else cout<<"-1";
}浪费在哪里了呢?
当没有比a[j]小的数字时,就会白白遍历一遍。
这其实是可以避免的。
例如:
1,6,5,7,9
如果比如当遍历的6时,6比5大,所以,再往后,不可能有一个数字左边第一个比他小的数字是6了,因为有5,所以6就可以抹掉(出栈)
这时候需要用到单调栈,一个单调递增栈,
每次判断新入栈的元素是否比栈顶元素小,如果新入栈的元素比栈顶元素小,就弹出栈顶元素。
while(!empty()&&a[top]>=newnum)top--;
然后 栈顶元素就是当前元素左侧的第一个比当前元素小的元素
如果栈为空,那就不存在,就输出-1。
然后再将当前元素入栈
AC代码
#include<bits/stdc++.h>
using namespace std;
int sk[1000000];
int top=-1;
void push(int x)
{
sk[++top]=x;
}
void pop()
{
top--;
}
bool empty()
{
if(top<0)return true;
return false;
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int x;
scanf("%d", &x);
while(sk[top]>=x&&!empty())pop();
if(empty())printf("-1 ");
else {
printf("%d ",sk[top]);
}
push(x);
}
return 0;
}队列
模拟队列
手写队列的好处就是可以访问队尾元素,比如滑动窗口这道题就需要用到直接访问队尾元素
int sk[1000000];
int front=0,rear=-1;
void push(int x)//入队
{
sk[++rear]=x;
}
void pop()//队头出队
{
front++;
}
void pop_rear//队尾出队
{
rear--;
}
bool empty()//判断是否为空
{
if(rear<front)return true;
return false;
}
int querey()//队头元素
{
return sk[front];
}
int querey_tail()//队尾元素
{
return sk[rear];
}单调队列
单调队列,也是维护一个满足单调性的队列。
从头到尾单调递增:
每次入队前,判断入队元素与队尾元素的大小。如果入队元素小于队尾元素,就将这个队尾元素抹去。直到队尾元素大于入队元素或者队列为空。这样的话从头到尾就是单调增的
例题:
给定一个大小为 n≤106的数组。
有一个大小为 k的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k个数字。每次滑动窗口向右移动一个位置。
以下是一个例子:该数组为 [1 3 -1 -3 5 3 6 7],k为3。
| 窗口位置 | 最小值 | 最大值 |
|---|---|---|
| [1 3 -1] -3 5 3 6 7 | -1 | 3 |
| 1 [3 -1 -3] 5 3 6 7 | -3 | 3 |
| 1 3 [-1 -3 5] 3 6 7 | -3 | 5 |
| 1 3 -1 [-3 5 3] 6 7 | -3 | 5 |
| 1 3 -1 -3 [5 3 6] 7 | -3 | 6 |
| 1 3 -1 -3 5 [3 6 7] | -3 | 7 |
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 n和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n个整数,代表数组的具体数值。同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
输入样例:
8 3
1 3 -1 -3 5 3 6 7
输出样例:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
思路就是 维护一个长度为K的队列,
暴力做法的话
for(int i=front;i<=rear;i++)
{
if(maxans<a[i])maxans=a[i];
}就是每次遍历这个队列,找到最小的或者最大的。那就是O(n*k)的复杂度。
单调队列的做法呢?
例如求最小值。我们需要一个单调递增的队列,这样队头就是最小的元素。
维护的时候。
例如给定数组
1,4,6,3,4,5
该数组对与队列中的两个元素,到3要入队时,3比队尾元素6小,则对于往后只要6在窗口中,3一定在。这样的话,6就永远不可能是窗口中最小的值,所以6就可以从队尾剔除了,之后队尾是4,还比3大,继续剔除,然后将3入队,队尾就成了3。输出队头,1是最大的
while(!q.empty()&&newnum<q.rear())
{
q.pop_rear();
}AC代码
#include<bits/stdc++.h>
using namespace std;
int a[10000000];
int q[10000000];
int front=0,rear=-1;
void push(int x)//入队
{
q[++rear]=x;
}
void pop()//队头出队
{
front++;
}
void pop_rear()//队尾出队
{
rear--;
}
bool empty()//判断是否为空
{
if(rear<front)return true;
return false;
}
void clear()
{
front=0,rear=-1;
}
int main()
{
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
while(!empty()&&a[i]<q[rear])
{
pop_rear();
}
push(a[i]);
if(i-k>=1&&a[i-k]==q[front])pop();//当i-k>=1时,说明队列已经维持在k以上个了,
//当a[i-k]==q[front],则下一步,队头就不在这个滑动窗口内了
//因为这里是一次走一步,所以可以if判断,换成while也可以
if(i-k>=0)cout<<q[front]<<" ";//判断队列元素够不够k个,够的话就是输出队头,就是最小值。
}
puts("");
clear();//清空一下队列
//反之亦然
for(int i=1;i<=n;i++)
{
while(!empty()&&a[i]>q[rear])//这里改一下就行
{
pop_rear();
}
push(a[i]);
if(i-k>=1&&a[i-k]==q[front])pop();
if(i-k>=0)cout<<q[front]<<" ";
}
}