1.从全连接层到卷积
我们都知道CNN擅长的是处理图片,但是传统的神经网络肯定也是可以处理图片的,那么CNN的优势在哪呢?
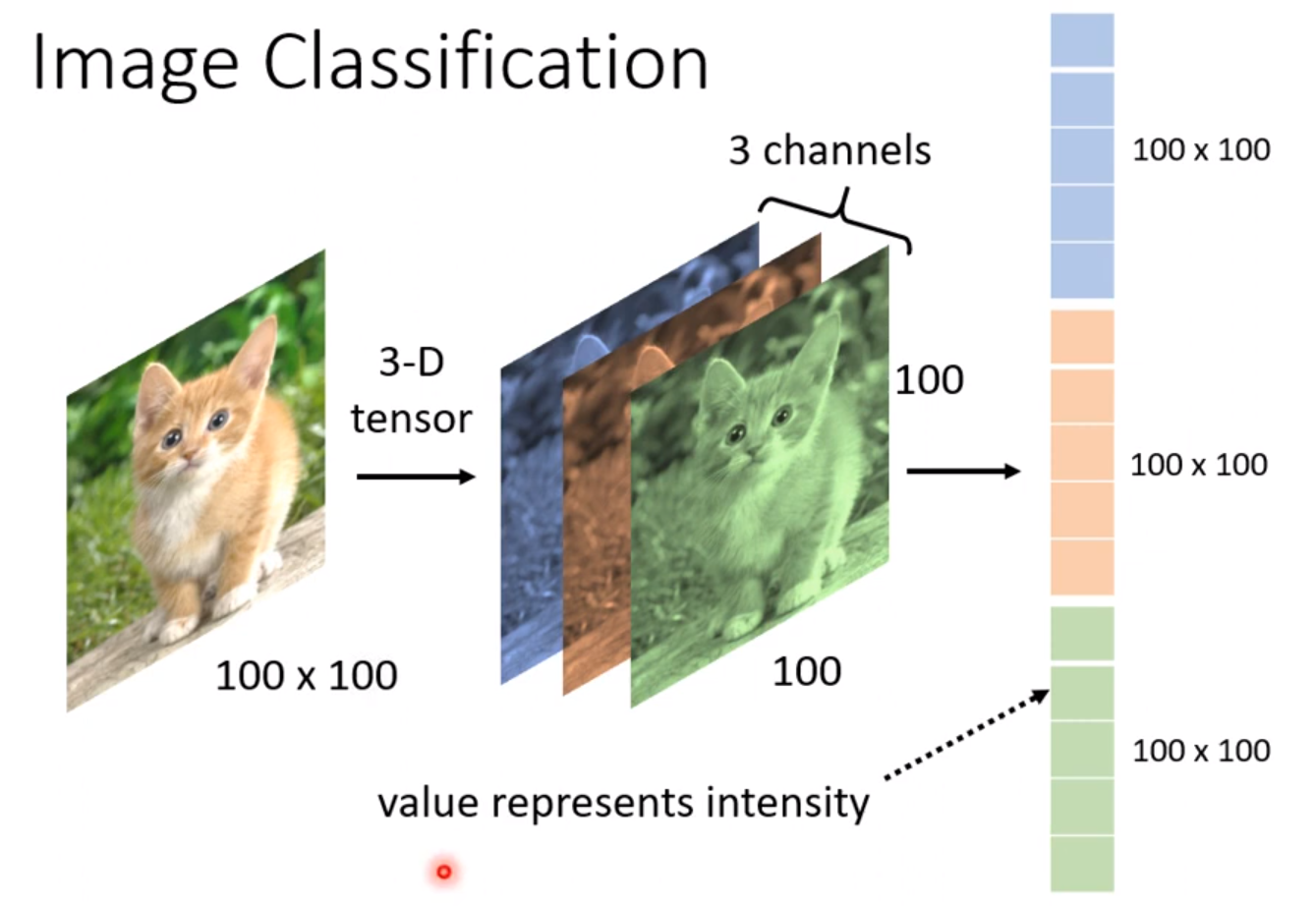
对于一张彩色RGB图像,他有三个颜色通道,传统的神经网络的做法就是将三个通道的颜色强度分别作为输入。如下图所示。
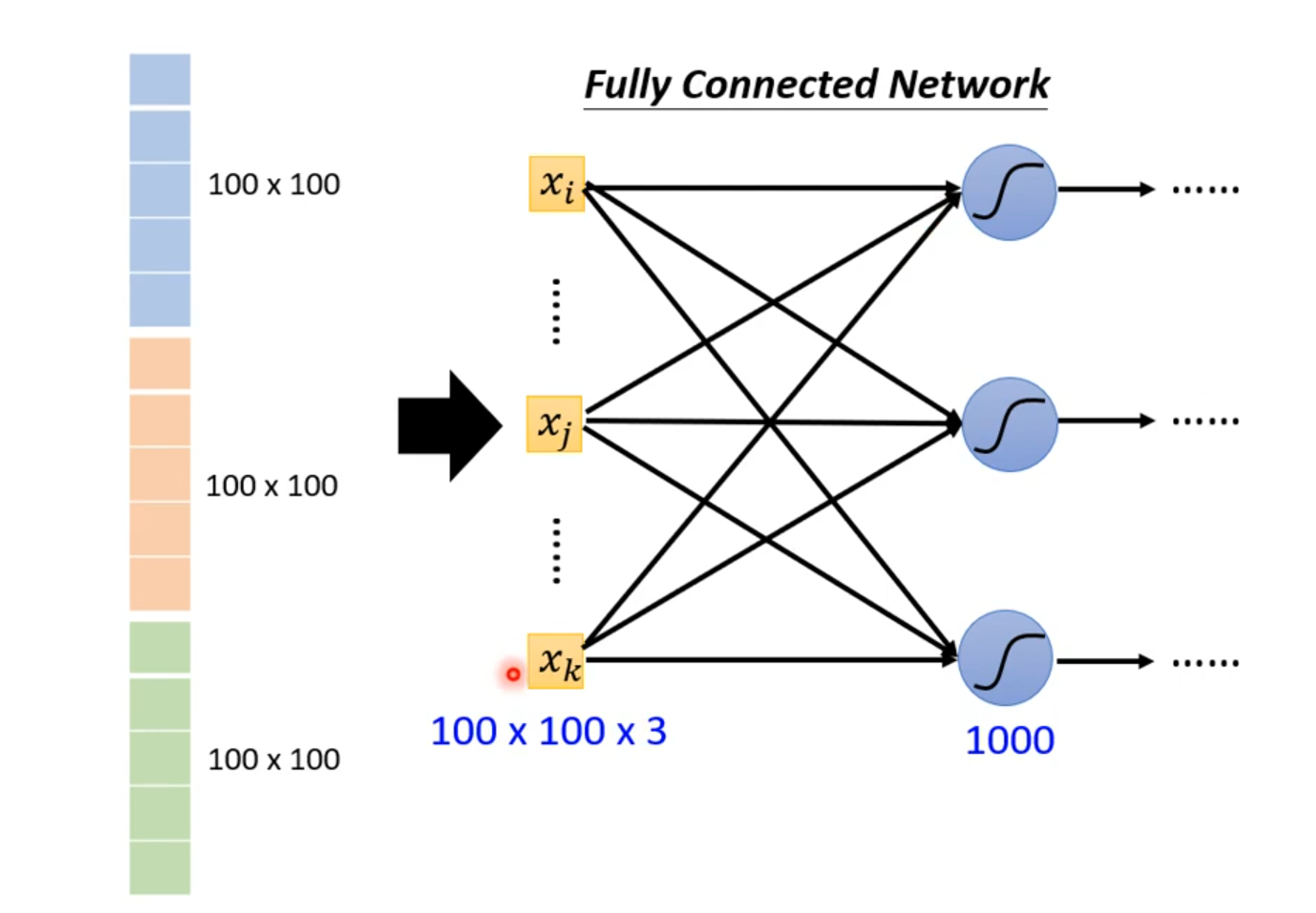
可以得出,输入层的特征向量数量为100×100×3,再加上隐藏层的神经元个数,那就是$100×100×3×1000=3^7$个weight。
其实考虑到我们人眼识别物体,很多时候也是识别一些特征,就比如下图:

乍一看,好像是一只乌鸦,因为我们看到了"鸟嘴"。所以有时候只需要看图片的一小部分,就可以侦测到比较关键的信息,就可以识别图片到底是什么了。
在CNN中有这么一种方法:设定一个区域,叫做Receptive field。 每个Receptive field都只观察自己区域的特征就好了
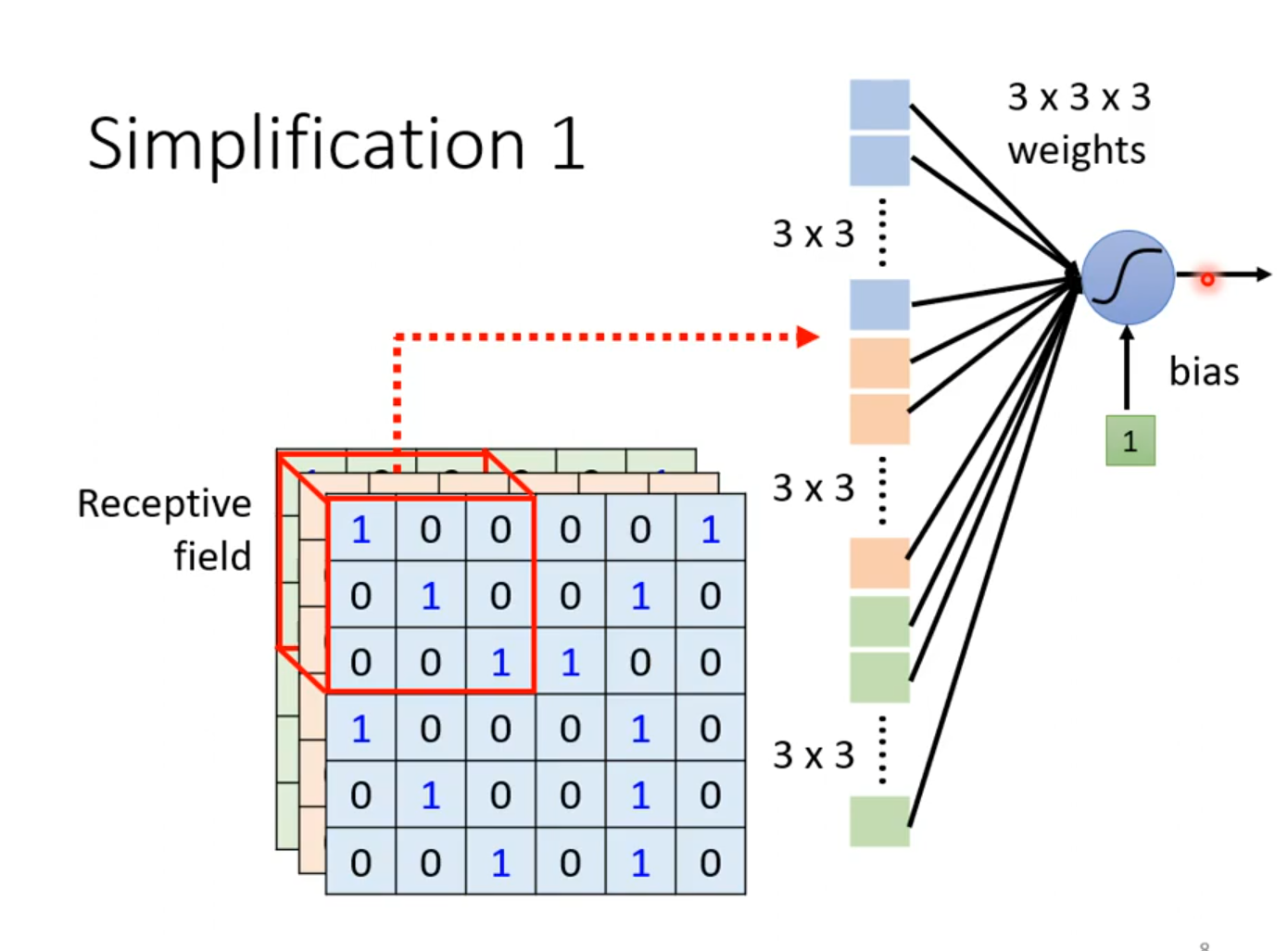
多个Receptive field之间是可以重叠的。
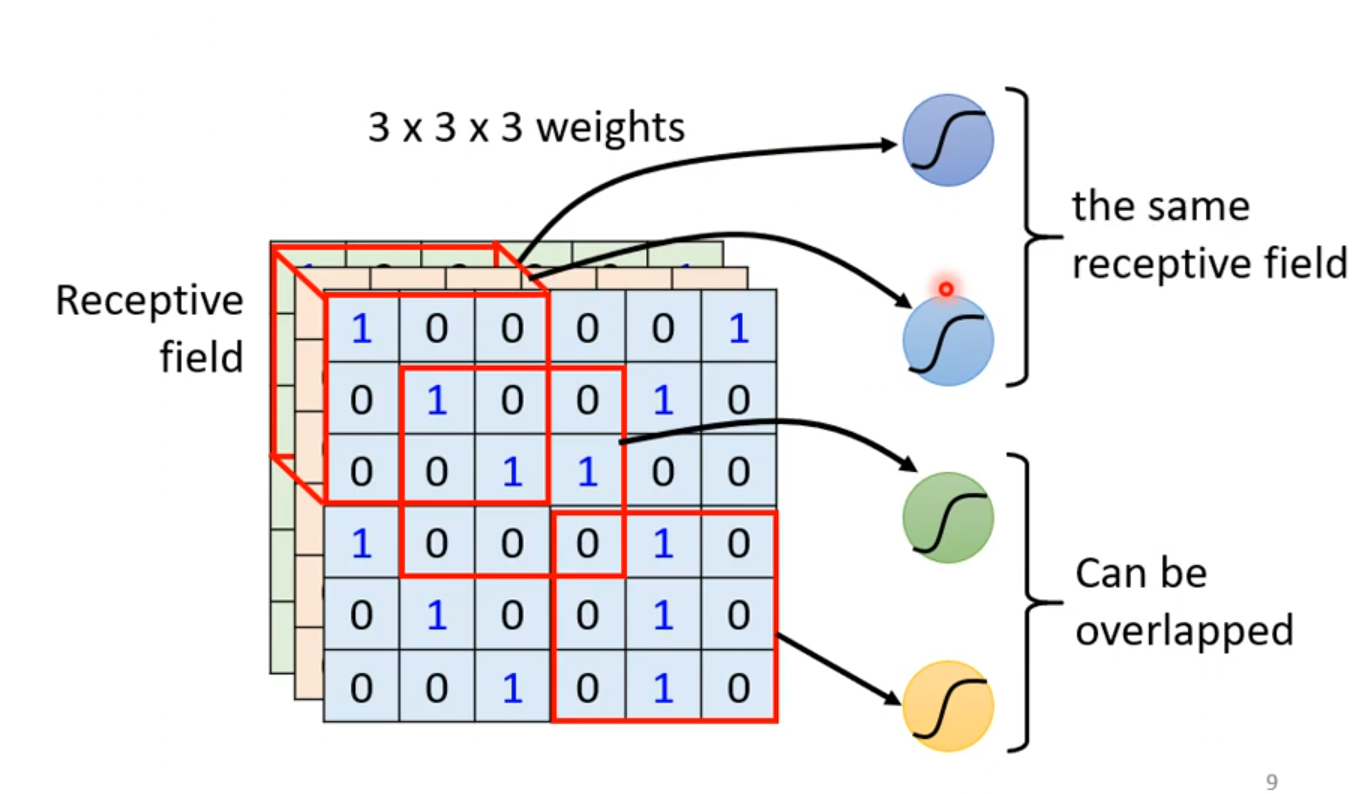
这个Receptive field每次移动的距离叫做步长(stride),我们一般将步长设置为1或者2,因为我们希望这些Receptive field是高度重叠的,因为如果特征正好在两个field的交界处,我们可能就没法捕获这些特征了。当移动的距离超出了这个图像,我们就要进行在边缘进行填充,
一般进行补0
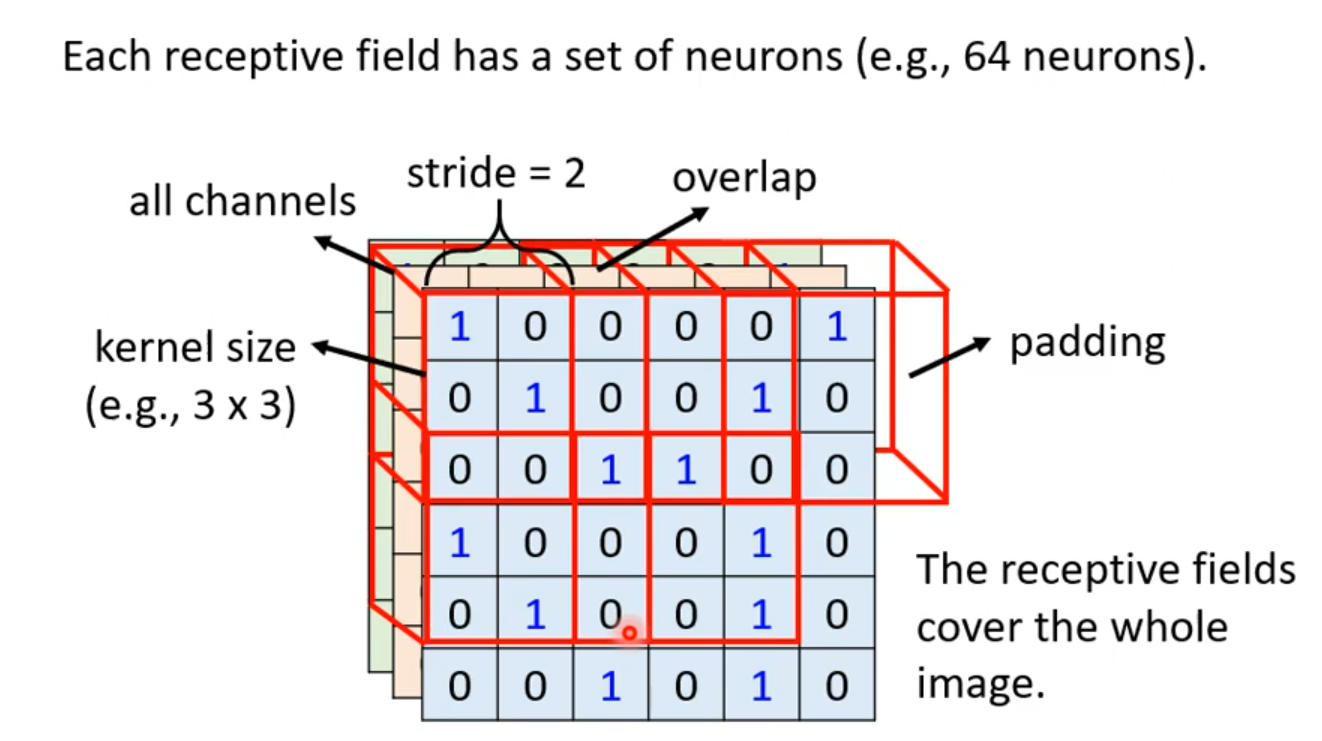
最终直到将整张区域覆盖。
但是我们会发现,相同的特征可能会出现在不同的Receptive field。
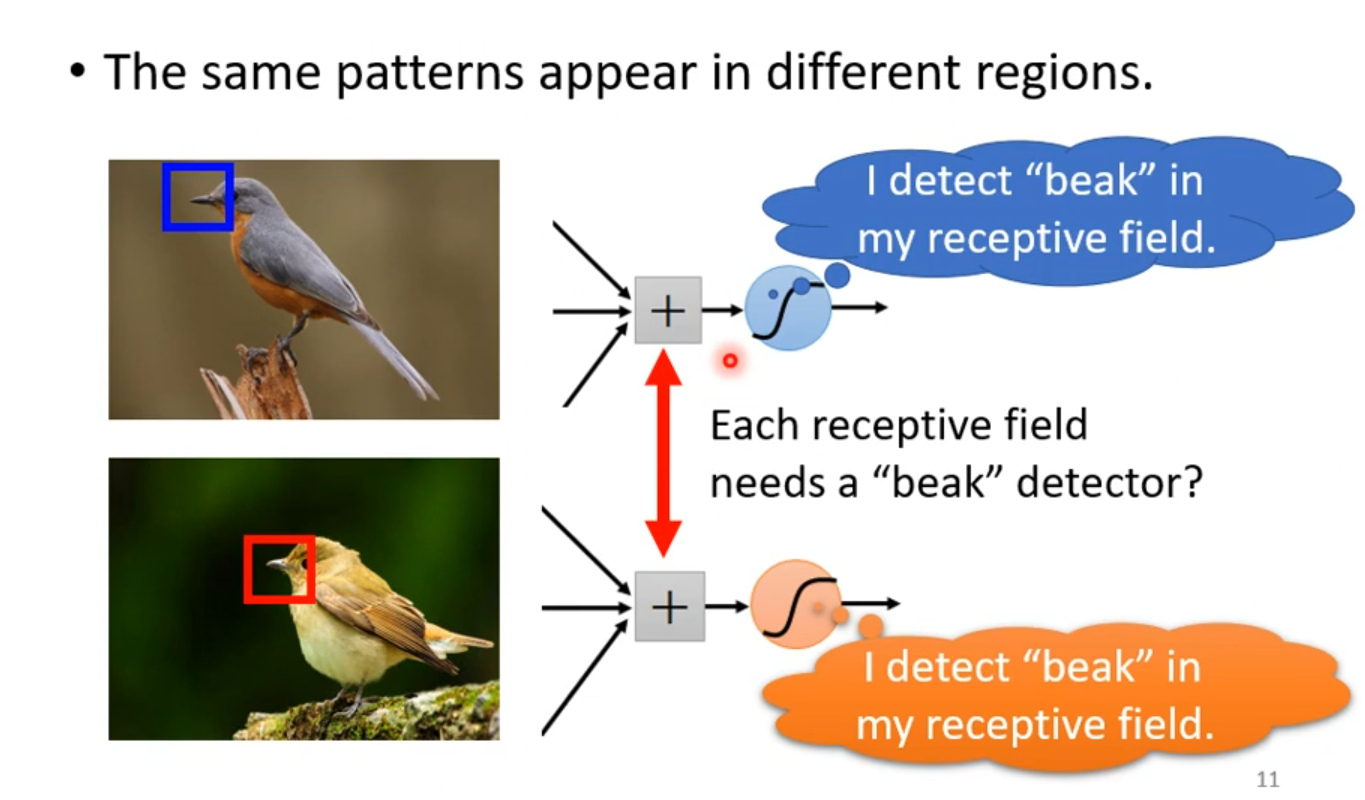
这样我们不一样的神经元的weight就记录了一样的特征,这似乎有些浪费。
这就引出一个概念:权值共享
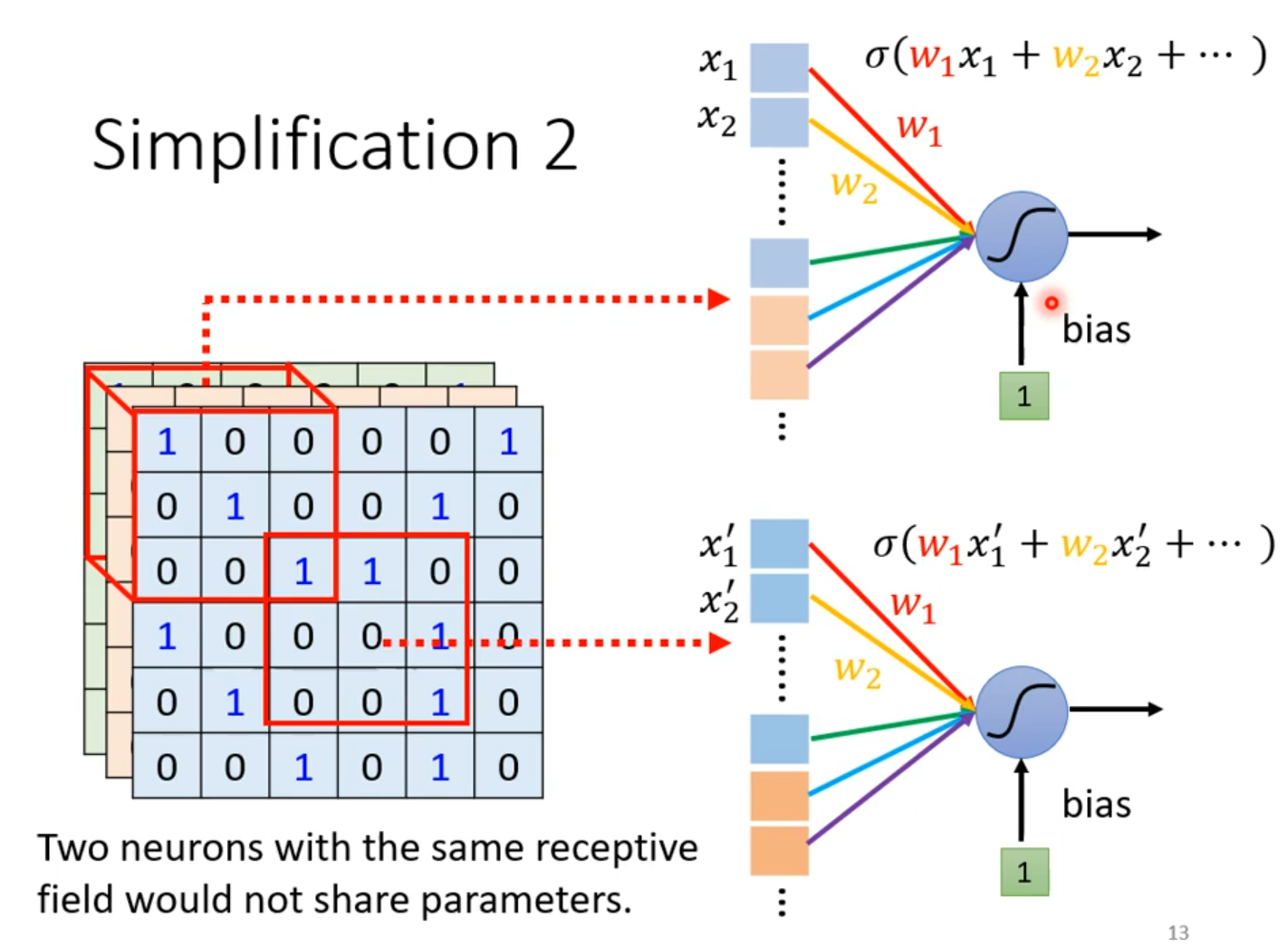
我们让一些Receptive field共享一样的权值。但是他们的输入值是不一样的,所以向后的输出也是不一样的。所以我们不能让相同的Receptive field具有一样的权值,否则输出就一样了。
那么什么样的两个Receptive field才共享参数呢?这里给出一个常用的方法:
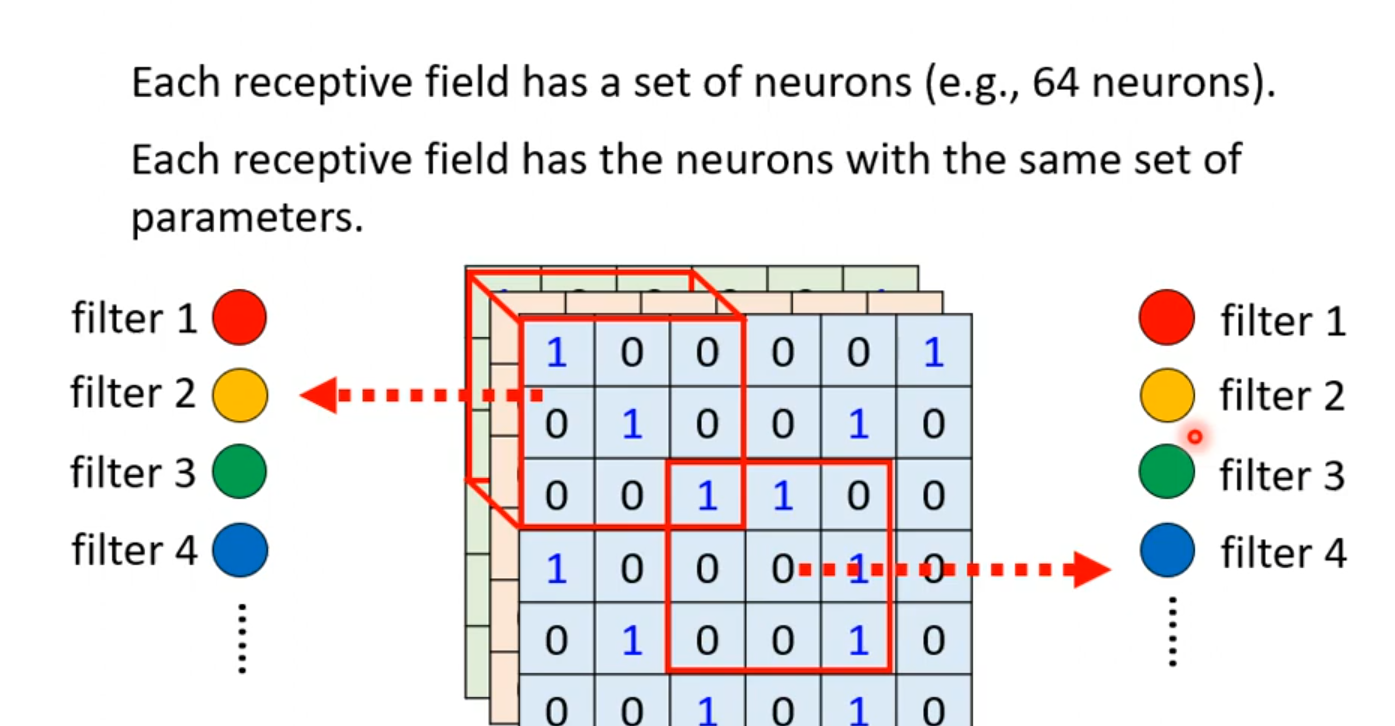
我们可以设定不同种类的的Receptive field,每一种类的Receptive field筛选出来的输出都具有相同的参数,这个时候,我们给这些不同种类的Receptive field起个名字:叫做filter。
2.卷积层(Convolutional Layer)
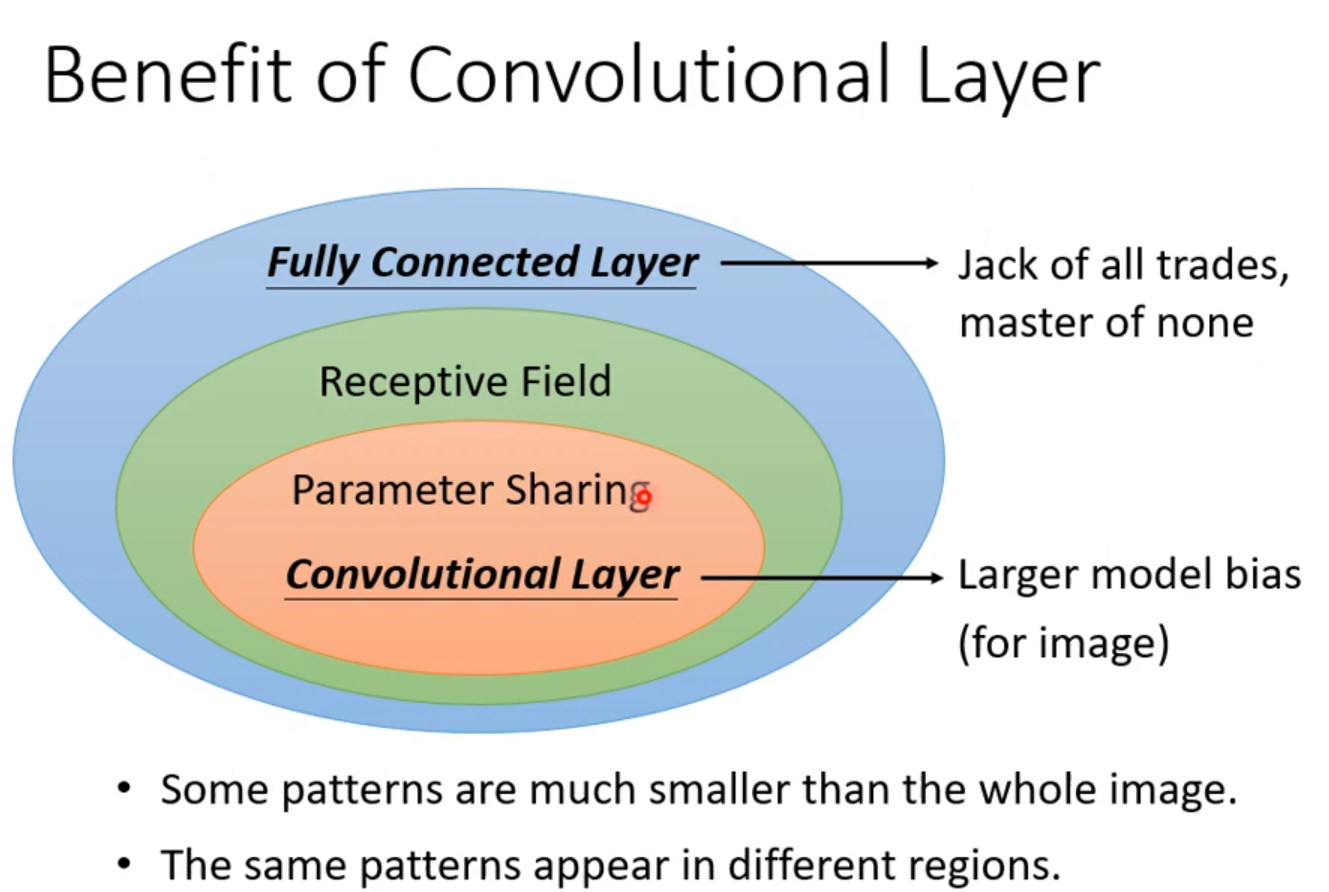
可以这么理解:Receptive field+权值共享就是卷积层。我们首先来看卷积层中最为重要的操作:卷积操作
卷积操作就是上面的Receptive field滑动的提取关键特征的具体体现做,Receptive field有个具体名字叫做卷积核,也就是上文中的filter
接下来我们先用二维矩阵来模拟卷积操作具体是怎么进行的,如下图所示
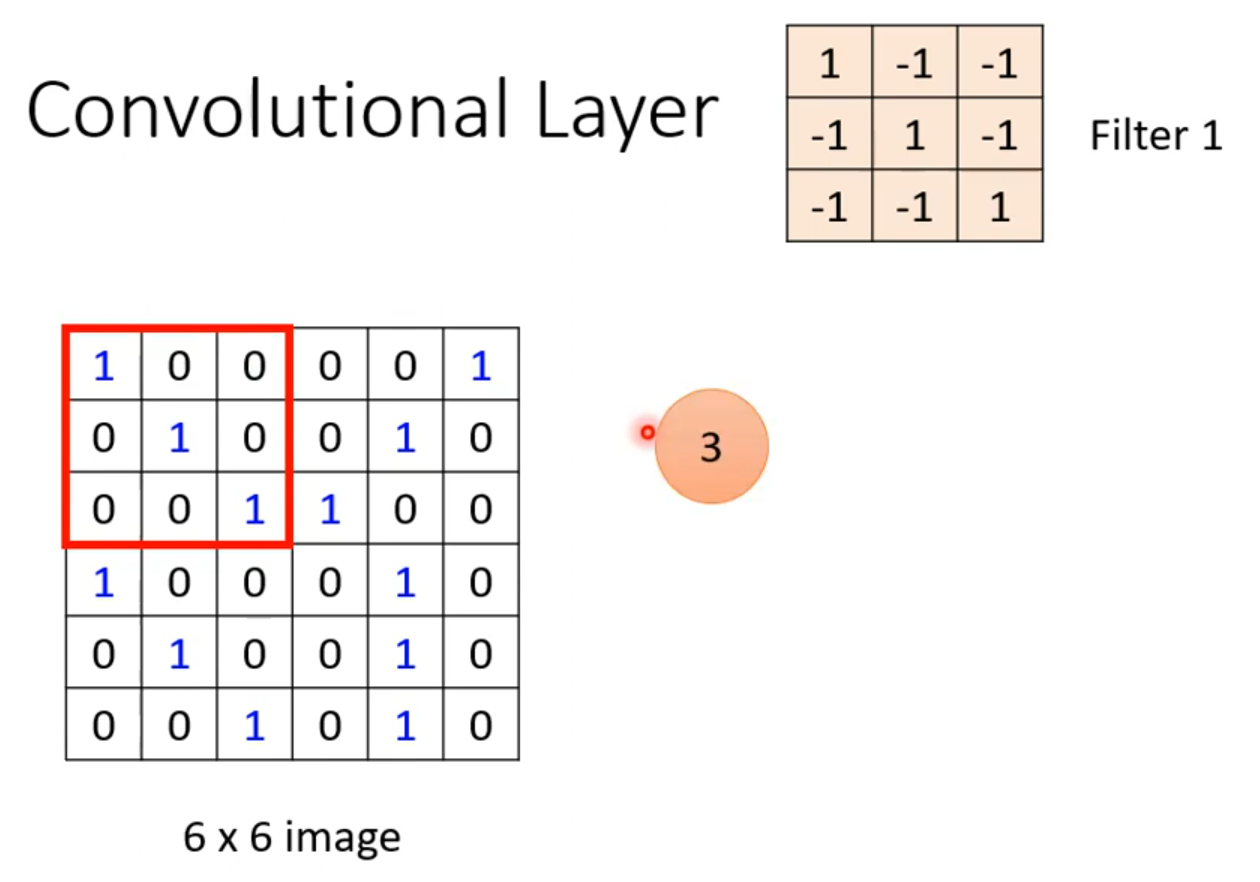
我们确定一个3×3大小的卷积核。
然后和左上角的3×3区域进行对应相乘再相加,得到3。写到右边的矩阵里,然后可以步长为1,那就是每次乘完,就向右边走一步。继续计算,得到-1
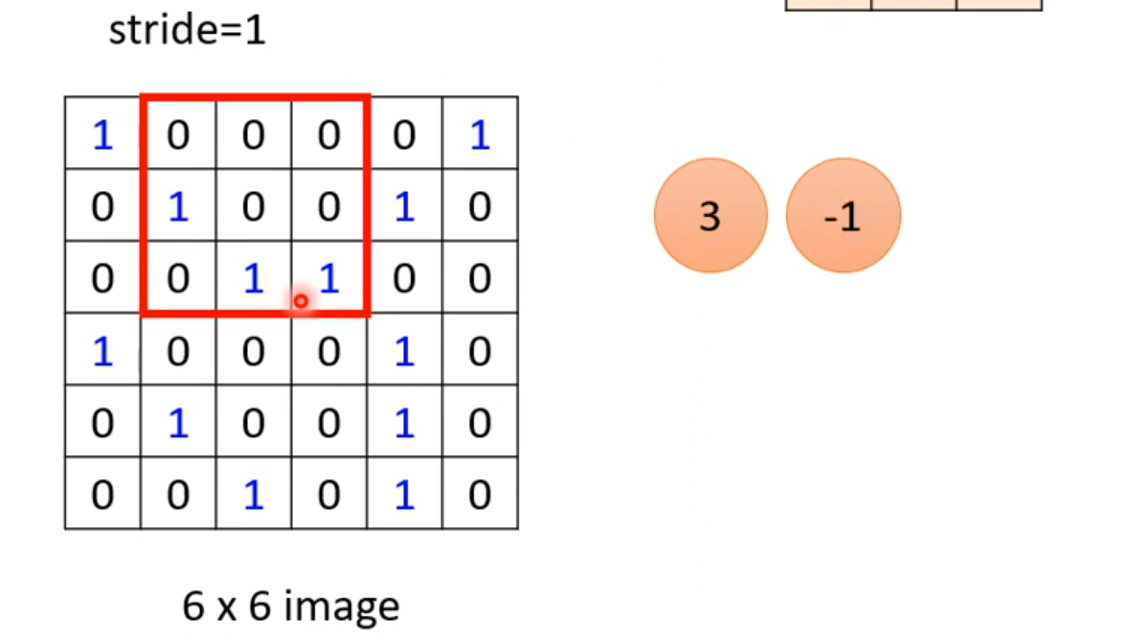
以此类推。得到最终的结果
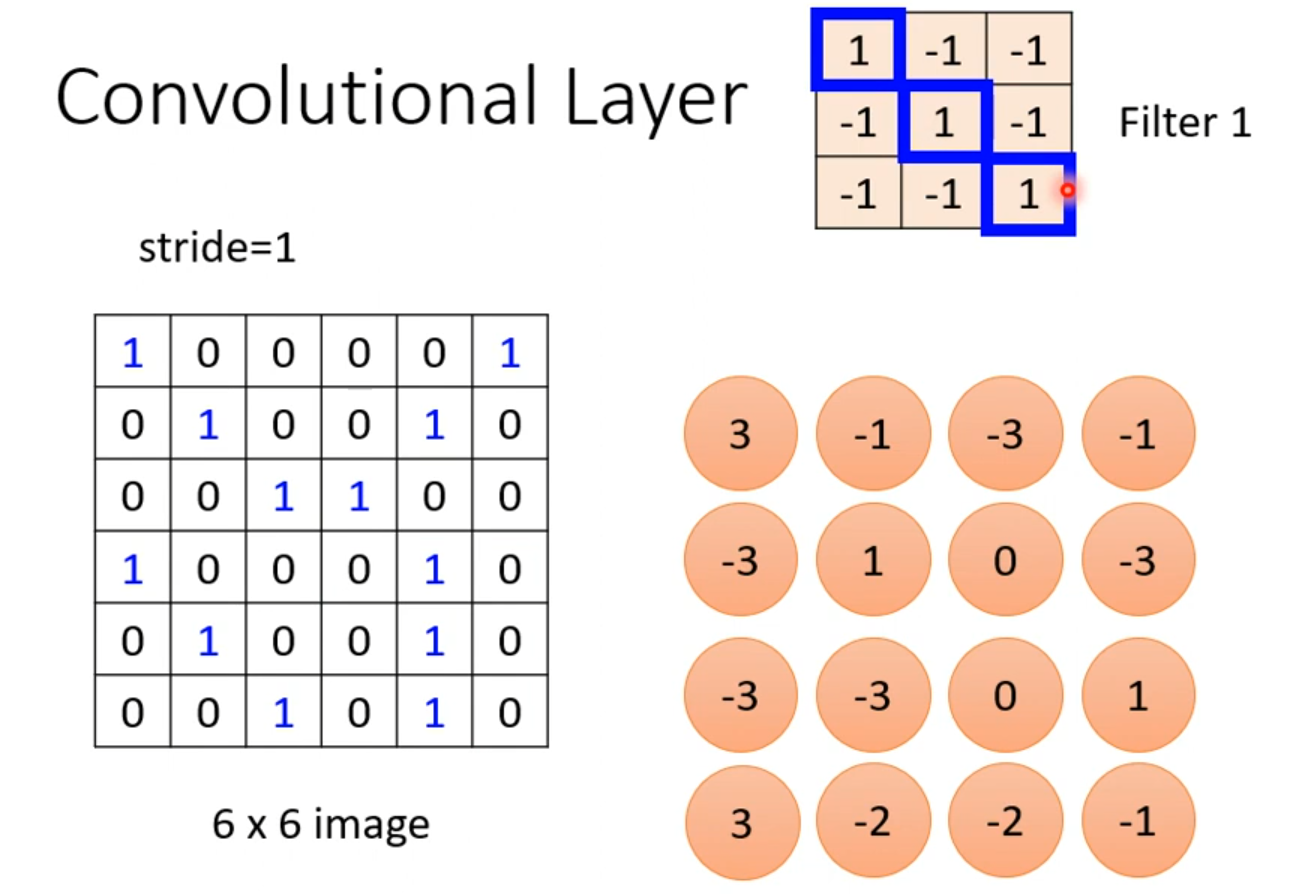
我们会发现,这里的的这个卷积核,他是的对角是1,其他为-1,那么这个卷积核就可以侦测同样是对角线都为1的区域,得到的数字为3。如下图,得到两个3,那么就可以判断那两个区域的对角线都为3,那么他们就可以共享同一个权值。也就是上文所说的权值共享
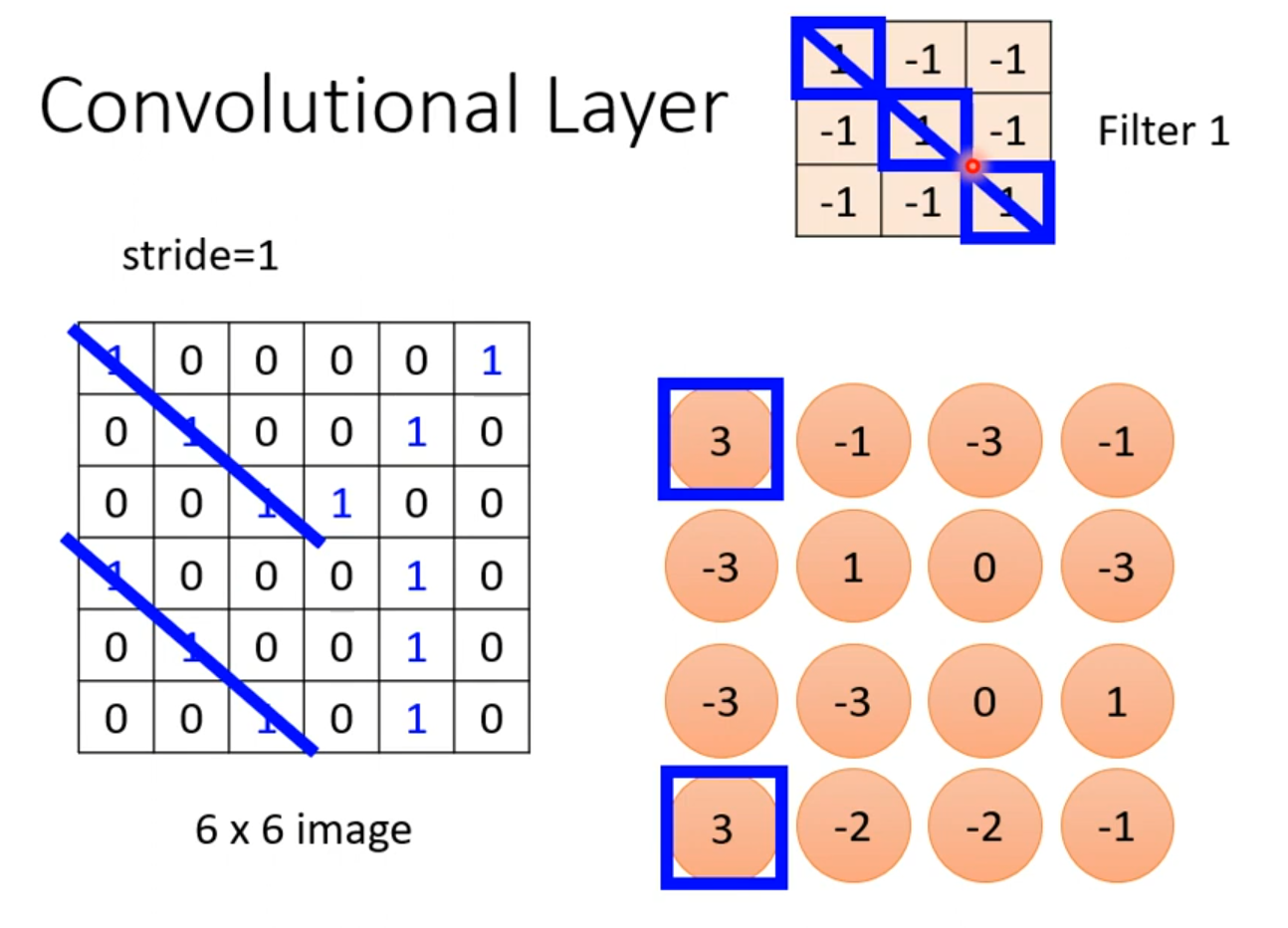
同样的我们也可以侦测第二列为1的区域,这样我们第二个卷积核就设定为第二列为1.如下图所示
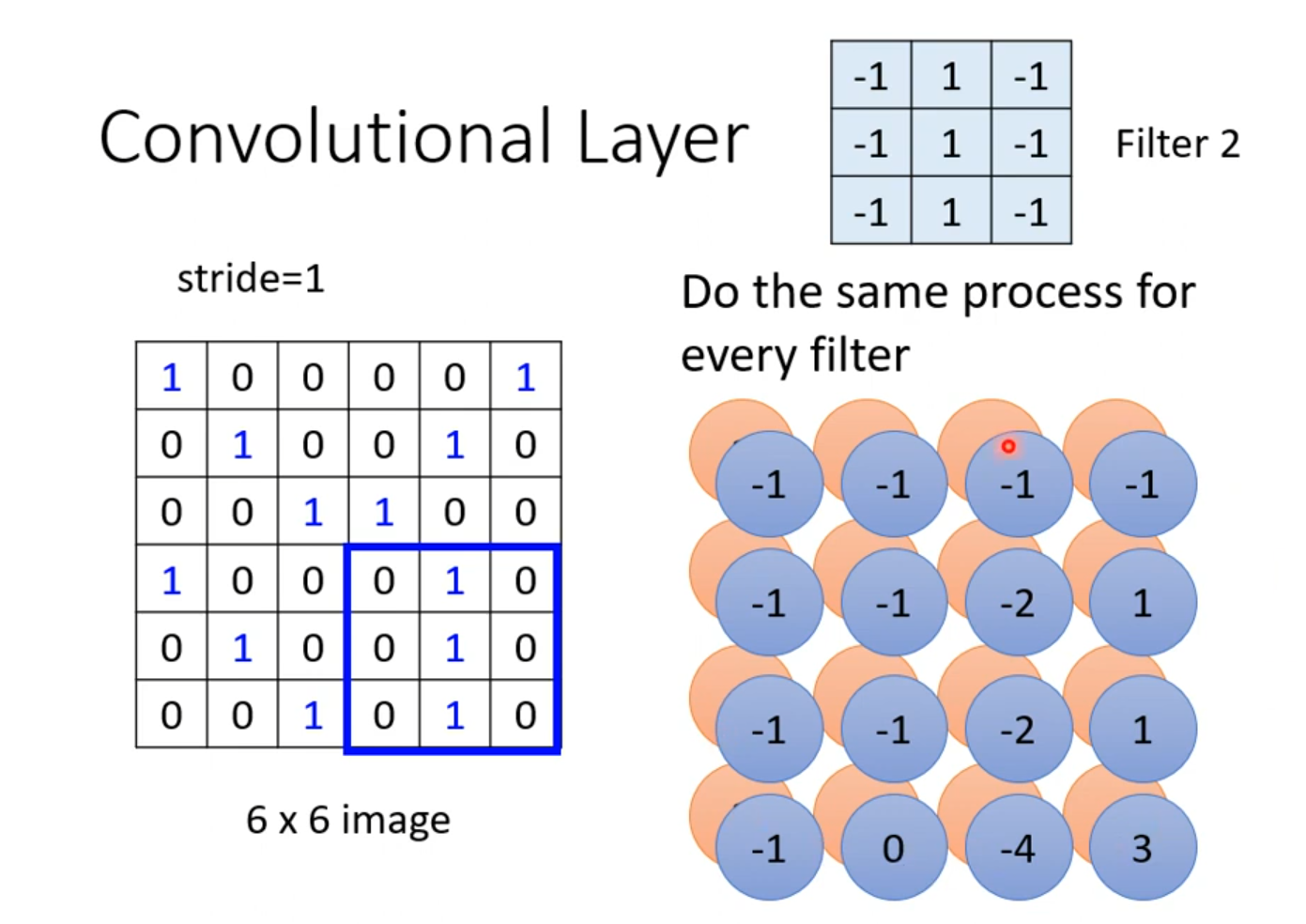
所以,我们设置多少个卷积核,那就会得到几个结果,我们把这些结果的集合叫做特征图(Feature Map)

以上只是有一个通道的图像,所以只是二维,我们将放到多通道图像上来看,如下图所示我们输入一个3×3大小的图像的RGB图像是三个通道,每个通道有3×3大小的图像。这里有两个理解:一个理解是3个3×3大小的卷积核为一组,分别对应三个通道,另一个理解是:卷积核就只有1个,大小为3×3×3,高度为3,而这个高度就正好是图片的通道大小。下文我就用第一种理解来叙述了;我们得到的特征矩阵(特征图)的每个值是该组卷积核中,每个卷积核在滑动过程中在对应位置得到的值再相加得到的,如图:卷积核1中三个卷积核在滑动过程中,得到左上角的数分别为:1×0+0×1+0×0+0×0=0,0×0+1×0+0×1+0×0=0,0×1+0×0+1×1+0×1=1,所以这三个数加起来得到黄色矩阵的左上角结果为1,以此类推就得到所有的特征图了。所以,有几组卷积核,特征图就有几维
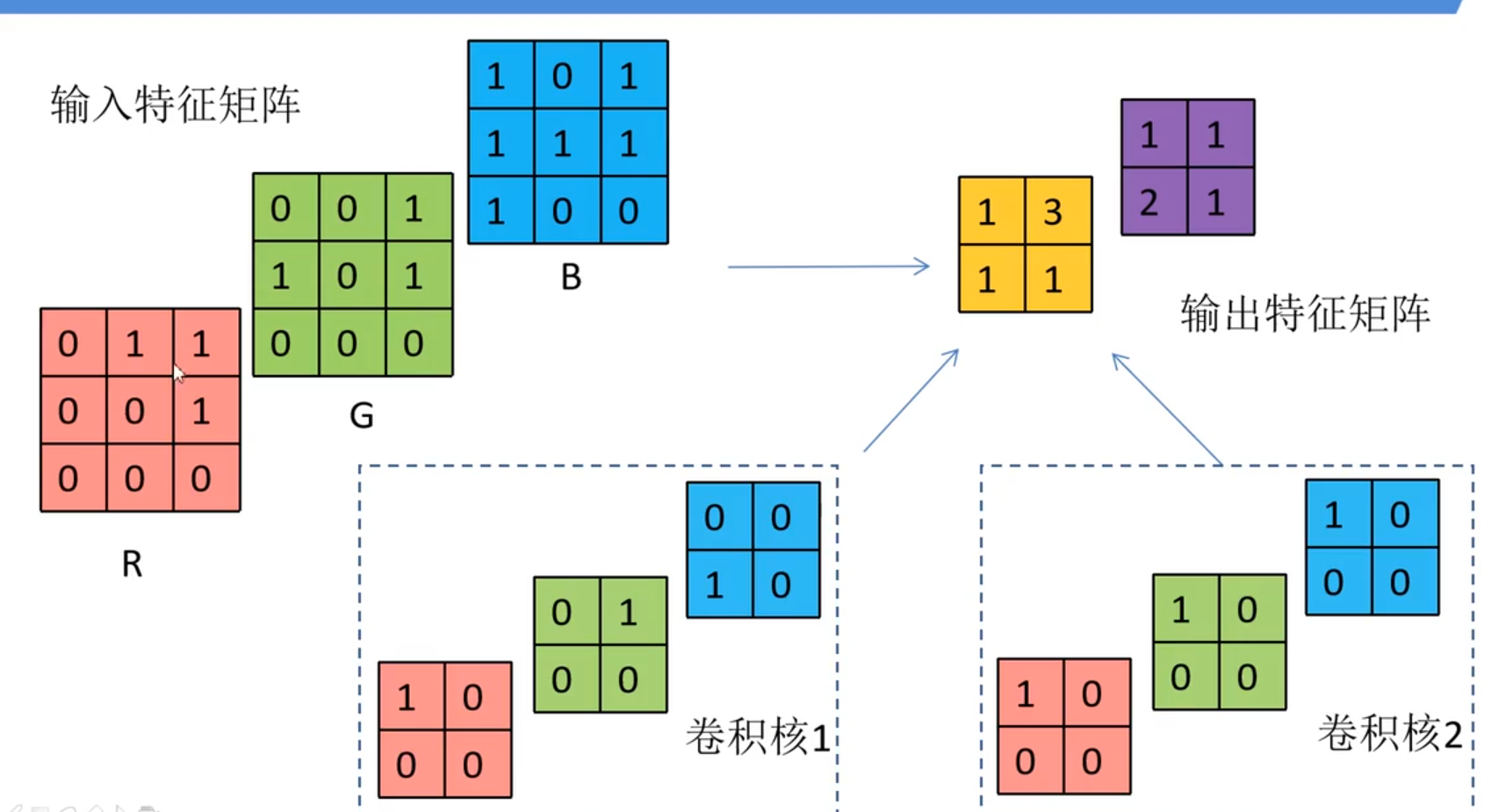
卷积层也可以多层进行叠加:但是第二层的卷积核数量就必须和第一层的数量一样(或者说高度相同)
3.池化层
在进行卷积操作得到的特征图之后,我们还需要对特征图进行稀疏处理,以减少数据运算量。
常见的几个处理方式:
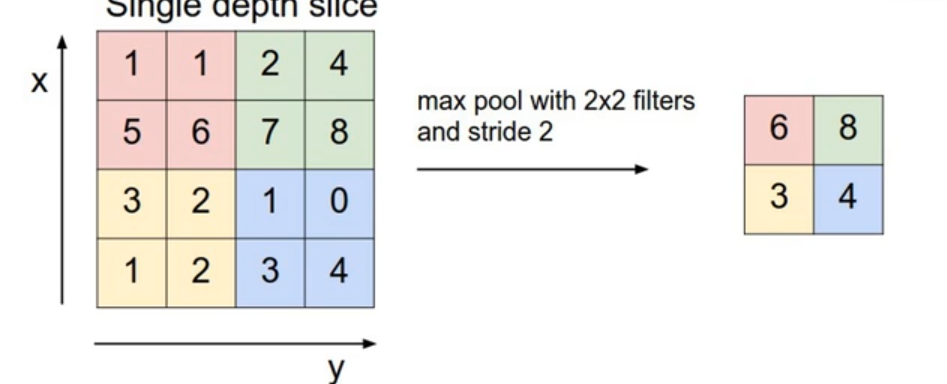
MaxPooling 最大池化层
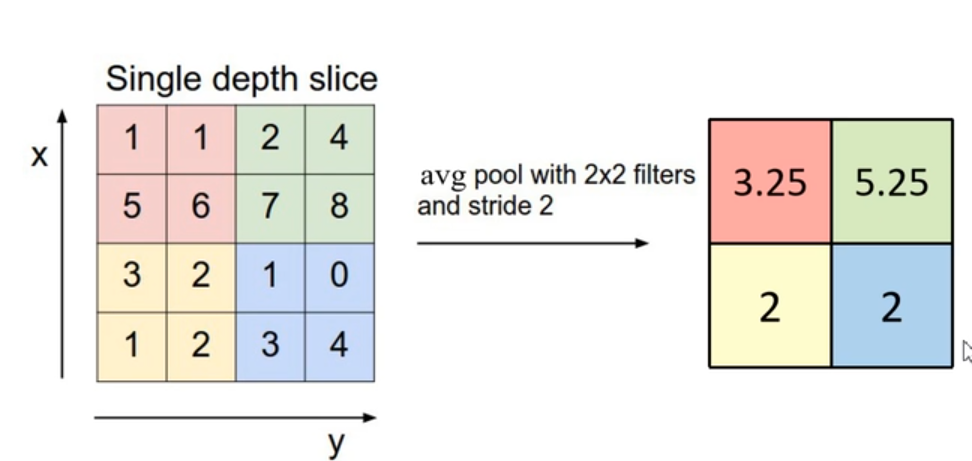
就是将特征图分为几组,每一组取最大的那个,进行降维处理MeanPooling 平均池化层
具体采取什么池化方式都是自由的,包括划分区域也不一定是2×2的区域。都是由我们自己决定的。但是一般poolsize和stride是相同的。
池化层的最大作用就是减少数据运算量,但是可能会损失一些特征,在算力飞速发展的今天,有些架构会取消掉pooling层。
4.整个卷积神经网络的流程
上边我们经历了从输入图片->卷积层->池化层(中间可能会经过好多个池化层和卷积层)
再进行完这些之后,再将最后的结果Flatten一下,变成1维向量,就可以交给全连接层进行训练了,如下图所示
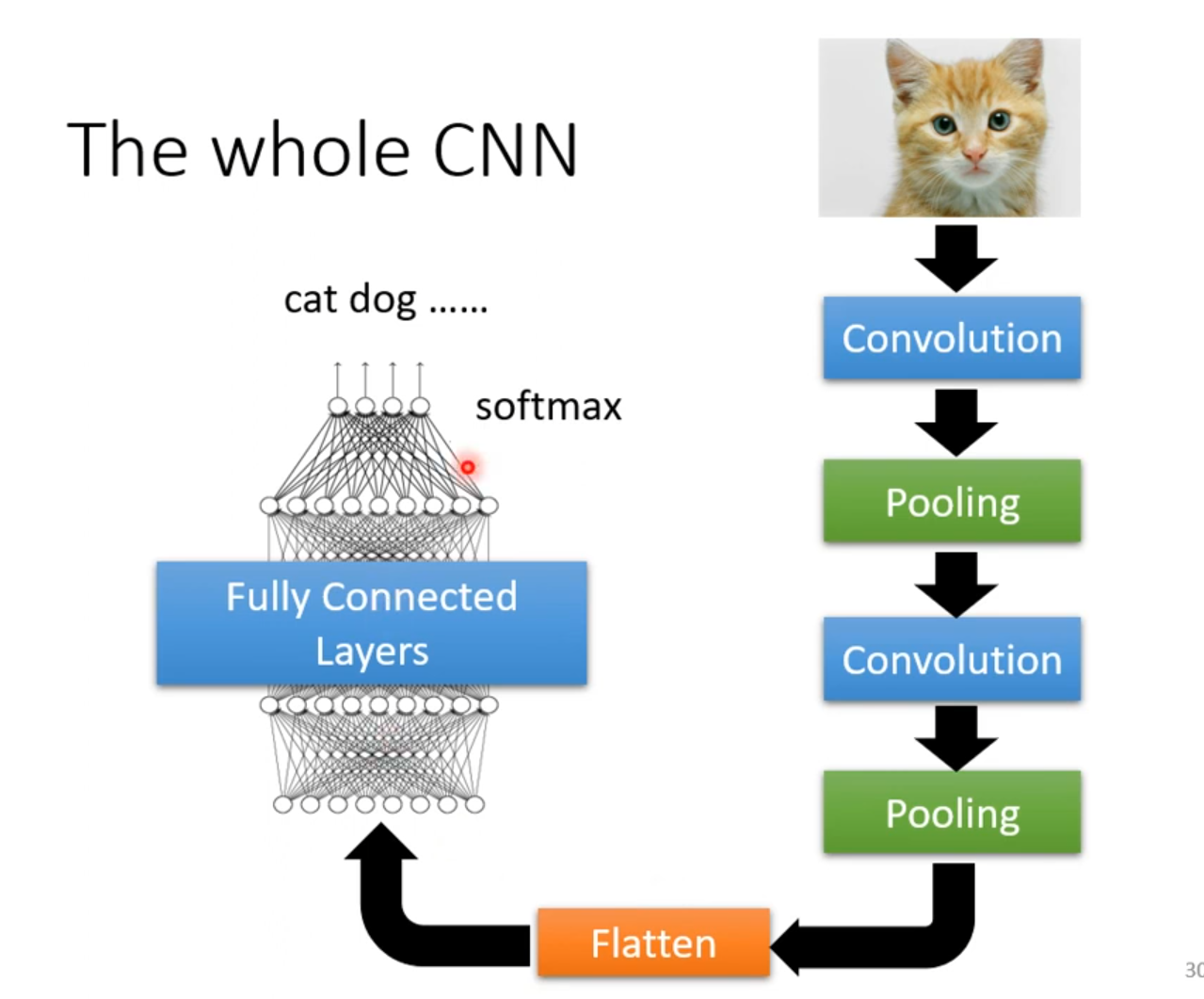
5.总结
对于图片,他最重要的特征就是像素点,这些像素点可以转为tensor,作为特征交给机器学习,但是分辨率极高的图片,他像素点的量是太多了,用传统的神经网络会有超级多的特征,模型复杂度会大大提高。所以我们需要对特征进行压缩,那就是对图片进行压缩,但是压缩会丢失很多信息,不利于模型的训练,这时候我们就要提取关键特征,用于模型训练,以达到更好的识别效果。怎么提取呢?这就是卷积操作。最后进行卷积、池化,得到一定数量的特征值,最后输入给全连接层,进行训练。
所以我真觉得发现这种方法的人是个天才,都不用查,一定是数学家想出来的。之前学习机器学习还着重于原理以及逻辑性,也就是为什么要这么做?现在看来,卷积这玩意的逻辑性和原理也不是我能理解的,我只要知道这么做就好了。。站在巨人的肩膀上了属于是