1.MLP与FNN的关系
在邱锡鹏老师的教材《神经网络与深度学习》中,介绍的第一个网络就是前馈神经网络(Feedforward Neural Network),接着是CNN(卷积神经网络),而在李沐老师的《动手学习深度学习》中,CNN的前一章节讲的是多层感知机(Multi_layer Perceptron),在我们学习的过程中,我们是可以把它们当作一个东西的,可以理解为MLP就是FNN,但是既然他们叫法不同,那一定是有区别的。
翻阅了很多资料:
WIKI百科上是这么解释的这俩概念:


结合其他资料
我大概总结了一下
FNN是指一种神经网络模型,其中信息从输入层流向输出层,不涉及循环或反馈。FNN可以是单层的(只有输入和输出层),也可以是多层的(有一个或多个隐藏层) FNN适合RNN对立的,所以只要符合信息单向传播的话,那就是属于FNN的,某种意义上来说,CNN也是属于FNN的(但是我们一般不这么说)。所以说,FNN是一个比较广义上的概念,MLP、线性神经网络都是属于FNN,但是MLP是FNN一个比较经典的模型,常常用来代表FNN了,说的多了,可能二者就混淆了。
2.问题的引出:解决非线性问题
前面学习了感知机算法,感知机算法有一个要求:数据必须是线性可分的。所以传统感知机算法是解决不了非线性问题的。我们以异或问题为例。
输入空间:$x_1$、$x_2$
输出:{1,0}
如果输入的两个数是相同的,那么输出0,否则输出1。
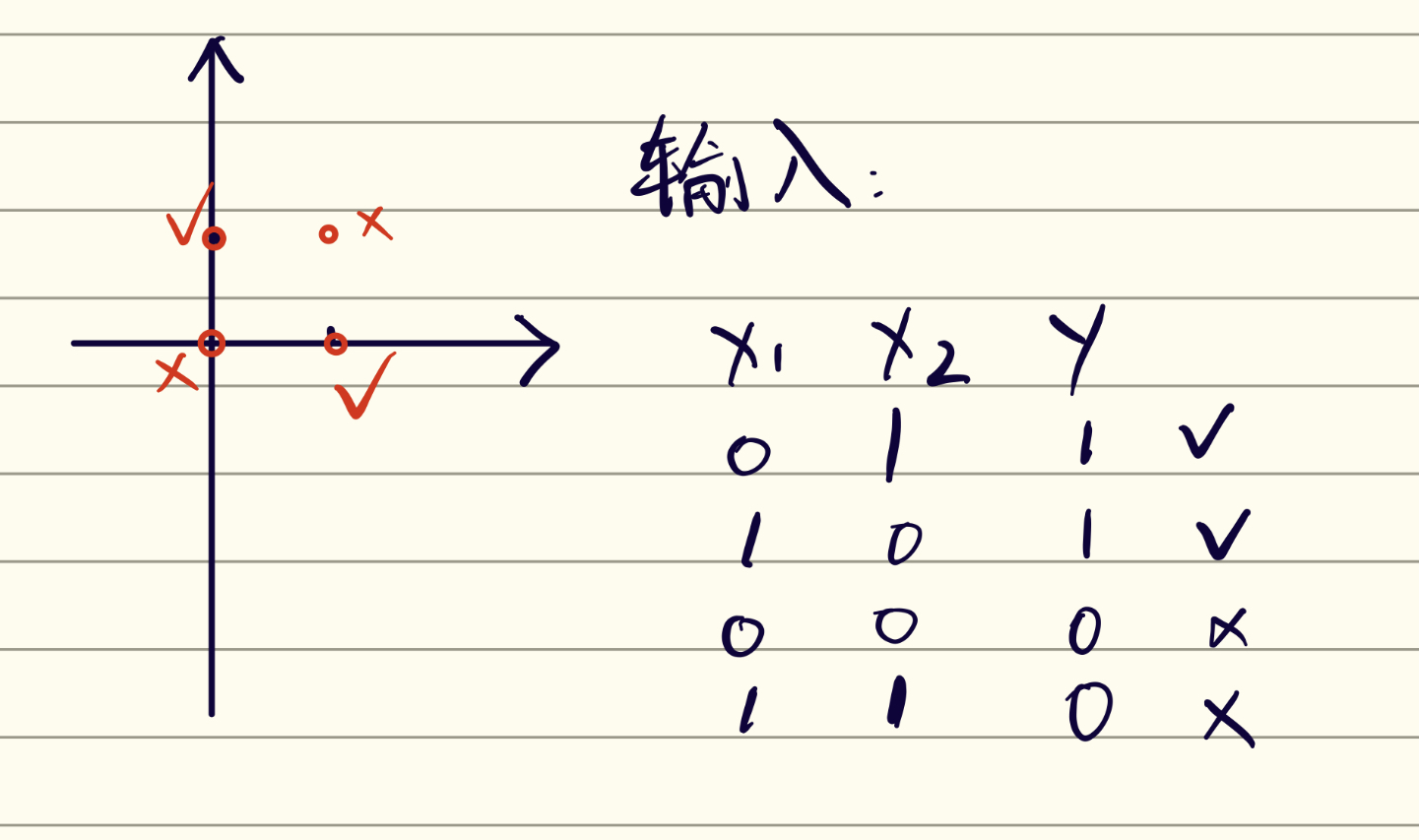
可以看到,当输入的为以上数据,那么在二维空间内是线性不可分的。那么感知机算法就是无法运用的。
传统非线性问题的解决
- 传统线性转换
Cover定理:将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。
根据该定理,我们可以把低维转换成高维,是更有可能形成线性可分的数据的。
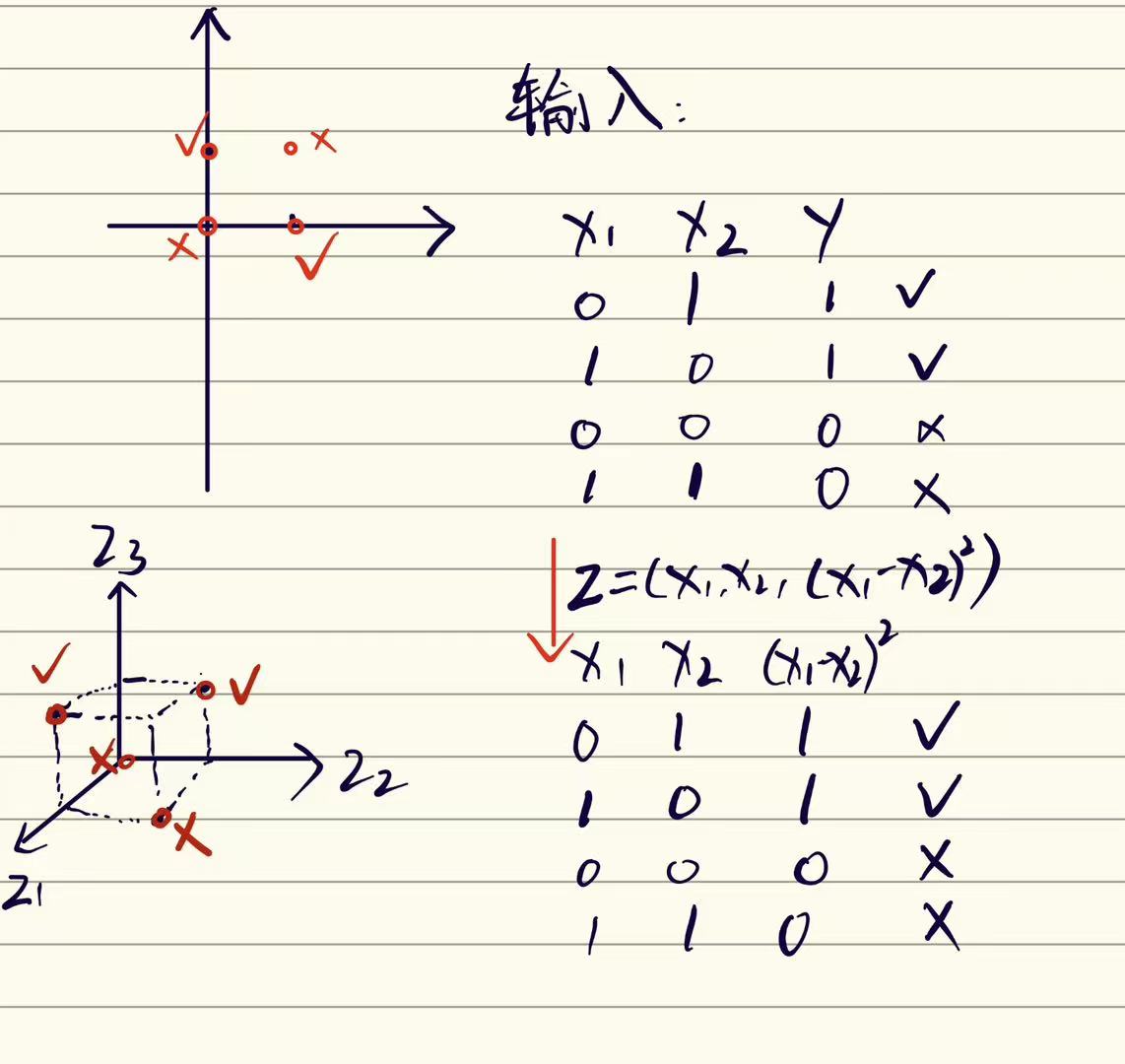
如图,以某种方法将二维转化成三维之后,我们可以把四个点以一个平面划分开
但是由于转换成高维空间的过程,我们要设计某种方法,转换成高维,这种方法需要设计,并且我们也不能保证转成高维之后就一定线性可分了,所以,这种方法的可行性有待商榷。
- 核方法
通过显式地引入核函数避开内积运算,核方法可以将特征变换的维度提升到无穷大,并将数据空间中的非线性问题转换成特征空间中的线性问题。
本人还没有学习SVM,所以对核方法也不是很熟悉,这里不再赘述
异或问题引出神经网络。
我们还是回到异或问题来。
根据离散数学所学,异或是复合运算,异或是可以由"OR"、"AND"和"NOT"表示的:
$$x_1\oplus x_2 = (\neg x_1\wedge x_2)\vee(x_1\wedge \neg x_2)$$
我们把$ (\neg x_1\wedge x_2)$看作①,$(x_1\wedge \neg x_2)$看作②,把最后的$\vee$ 看作③
我们可以画出以下图形
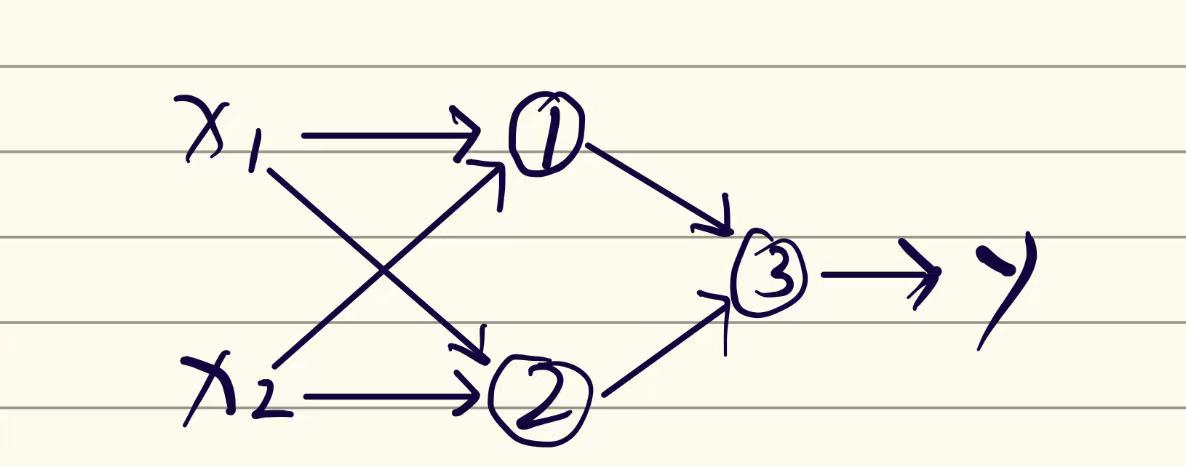
而因为①和②都是基本运算,基本运算是线性可分的(可以画个图证明一下),所以我们就将一个线性不可分问题拆成了两个线性可分的问题,最后两个问题再整合出来得到输出。
这张图中的$x_1和x_2$为输入层,中间的①和②为隐藏层。最后得到的y为输出层,而①、②、③这种被称之为神经元。
这大概就是一个神经网络的基本结构。他成功的解决了异或问题这样一个非线性问题。
3.从感知机到多层感知机
感知机模型也是可以画成神经网络结构如下图所示:

回顾一下感知机算法:
我们是要找到一个超平面将数据划分开
$$z=\sum\limits_{i=1}^mw_ix_i + b$$
带入特征之后得出一个target,target大于0的在这个平面的一端,小于0的在另一端。

从而得到我们想要的输出结果1或者-1。
但是,这样的神经网络过于简单,并且无法处理非线性数据。当我们要处理线性不可分的数据时,我们就可以类比上文对异或的处理方法,在输入层和输出层之间加一层隐藏层,这样我们就可以将非线性转换成线性。
如下图,我们多加了一层隐藏层,并且隐藏层的神经元个数为5,这样的就架构叫做多层感知机。

这个图中,层与层之间是全连接的,全连接的意思就是第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。
因为隐藏层和输出层都是全连接的, 所以我们有隐藏层权重$W^{(1)}$和隐藏层$b^{(1)}$以及输出层权重$W^{(2)}$和输出层偏置$b^{(2)}$,这样我们计算单隐藏层多层感知机的输出O为:
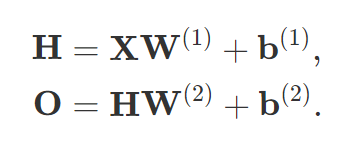
在上边那个单层感知机的神经网络模型中,在唯一一个神经元上有一个阶梯函数:

这个阶梯函数在神经网络中称之为激活函数
所以我们在进入隐藏层的之前,会将输入层的东西套一层激活函数:
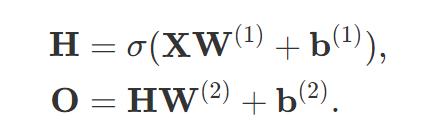
而隐藏层神经元个数以及层数这样的参数都是具体问题具体分析的,是由我们确定的,这样的参数叫做超参。我们也可以多加几层隐藏层:
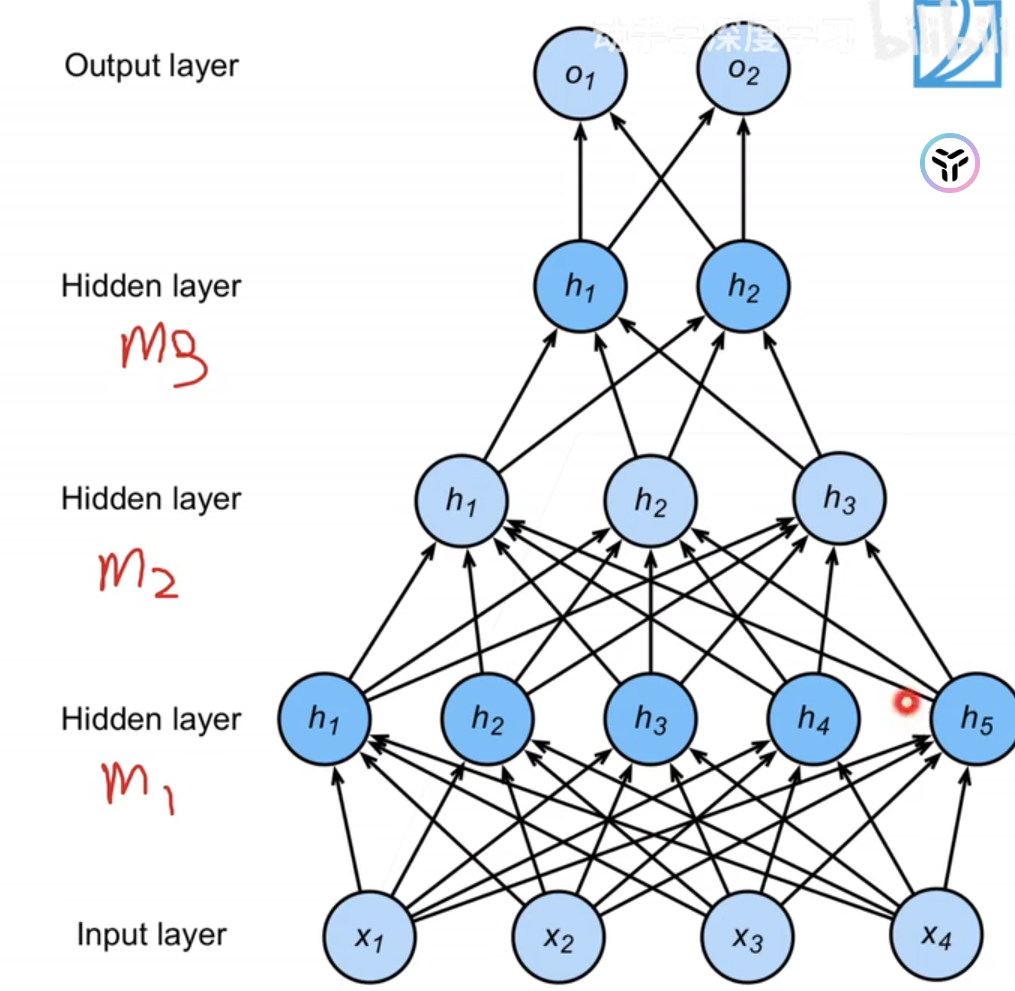
可以这么表示:
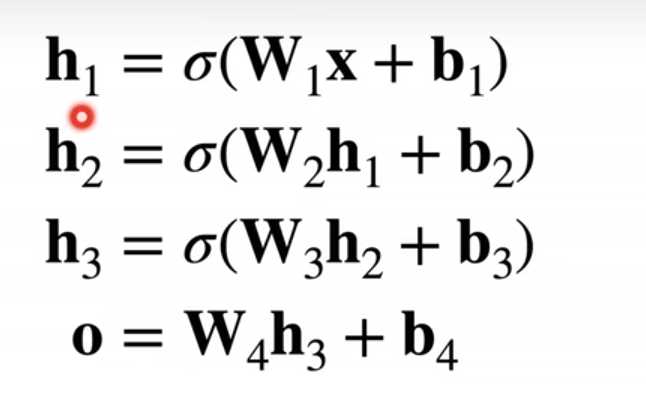
激活函数
激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。在神经元中,输入的input经过一系列加权求和后作用于另一个函数,这个函数就是这里的激活函数
激活函数最终决定了是否传递信号以及要发射给下一个神经元的内容
在单层感知机中,只有一个神经元,所以在该激活函数之后,就输出了。
这里用的激活函数比较落后了,在当今的神经网络中,我们也出现了一系列好用的激活函数:如Sigmoid、ReLU、等等。激活函数也是超参。
激活函数一般都是非线性的。
总结
大概对深度学习的深度有个了解了,突然明白为什么叫"炼丹"了,隐藏层神经元个数、层数等等这些超参,调起来好像没有什么理论支撑。。。但也是刚学,后边应该有更奇妙的东西。